Objectif
Comprendre les bases de la physique quantique, ses principes fondamentaux et ses implications.
Pourquoi c'est important ?
La physique quantique permet de

Annales

Annales
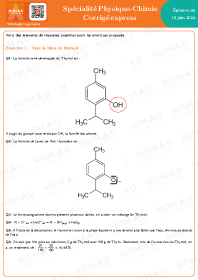
Annales

Annales

Annales

Annales

Annales
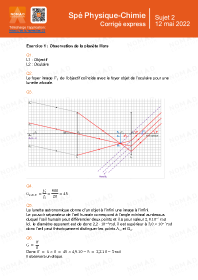
Annales

Annales

Annales
Comprendre les bases de la physique quantique, ses principes fondamentaux et ses implications.
La physique quantique permet de

Tableau d’avancement

Méthode tracés des vecteurs vitesse et accélération

Transferts thermiques

Transformations en chimie organique

Formulaire de Physique – Ondes et signaux

Mécanique
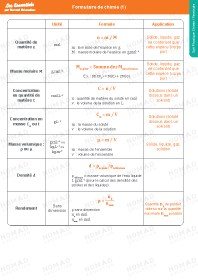
Formulaire de Chimie

Fiche outils
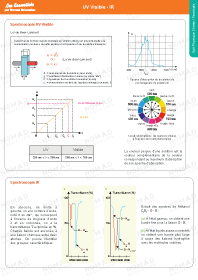
UV Visible - IR

Groupes caractéristiques

Mesures et incertitudes

Lunette astonomique - Dipôle RC
Un noyau instable (appelé noyau père) se désintègre spontanément en se transformant en un noyau d'un autre élément chimique (appelé noyau fils) en émettant une particule et éventuellement un rayonnement gamma.
| Particule émise | Symbole | Radioactivité | Équation |
| Électron | $\rm _{-1}^0e$ | $\beta^-$ | $\scriptstyle \rm ^A_Z X \rightarrow ^A_{Z+1} Y + ^0_{-1}e$ |
| Positron | $\rm _1^0e$ | $\beta^+$ | $\scriptstyle \rm ^A_Z X \rightarrow ^A_{Z-1} Y + ^0_{1}e$ |
| Noyau d'hélium 4 | $\rm _2^4He$ | $\alpha$ | $\scriptstyle \rm ^A_Z X \rightarrow ^{A-4}_{Z-2} Y + ^4_2He$ |
Le diagramme $\rm (N,Z)$ permet d'identifier le type de radioactivité et le noyau fils émis.

Au cours d'une transformation nucléaire il y a conservation du :
$\rm ^{210}_{84}Po \rightarrow ^{206}_{82} Pb + ^4_2 He$
Le nombre $\rm N(t)$ de noyaux radioactifs contenus dans un échantillon varie selon la loi.
$\boxed{\rm N(t) = N_0\cdot e^{-\lambda \cdot t}}$
Avec $\rm N_0$ nombre initial de noyaux radioactifs et λ constante radioactive en $\rm s^{-1}$ si $\rm t$ est en $\rm s$.
La demi-vie d'un noyau radioactif est égale à la durée au bout de laquelle la moitié des noyaux radioactifs initialement présents se sont désintégrés :
$\boxed{\displaystyle \rm t_{1/2} = \frac{\ln 2}{\lambda}}$
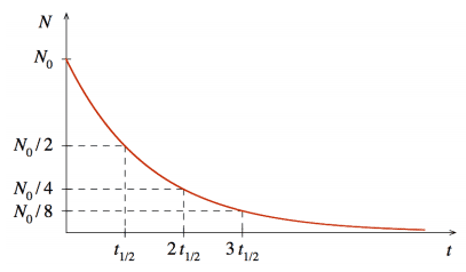
L'Activité $\rm A$ d'un échantillon radioactif est le nombre moyen de désintégration s'y produisant par seconde. Elle s'exprime en becquerel, noté $\rm Bq$.
$\displaystyle \rm A(t) = - \frac{dN(t)}{dt}$
Donc $\boxed{\rm A(t) = A_0e^{-\lambda t}}$ avec $\rm A_0 = \lambda \times N_0$.