Calcul intégral

Définition

On considère une fonction $f$ continue sur l'intervalle $[a ; b]$ ($a < b$) et on note $\mathrm F$ une de ses primitives. Cette définition établit le lien fondamental entre les primitives et les intégrales définies.

On a :

$$\int_{a}^{b} f(x) dx = [\mathrm F(x)]_{a}^{b} = \mathrm F(b) - \mathrm F(a)$$

Exemple

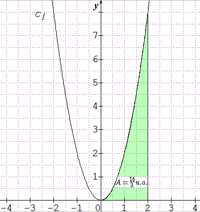
La fonction $f$ définie par $f(x) = 2{x}^2$ est continue sur l'intervalle $[0 ; 2]$ et une de ses primitives sur cet intervalle est la fonction $F$ définie par $\mathrm F(x) = \frac{2{x}^3}{3}$.

$$\int_0^2 f(x) \mathrm dx = \left[\frac{2{x}^3}{3}\right]_0^2 = \frac{16}{3}$$

Propriétés

Pour $f$ et $g$ deux fonctions continues sur l'intervalle $[a ; b]$ ($a < c < b$) et un réel $k$, nous avons les propriétés suivantes :

Linéarité de l'intégrale

Additivité :

$$\int_{a}^{b} (f(x) + g(x)) \mathrm dx = \int_{a}^{b} f(x) \mathrm dx + \int_{a}^{b} g(x) \mathrm dx$$

Homogénéité :

$$\int_{a}^{b} k f(x) \mathrm dx = k \int_{a}^{b} f(x) \mathrm dx$$

Relation de Chasles

$$\int_{a}^{b} f(x) \mathrm dx = \int_{a}^{c} f(x) \mathrm dx + \int_{c}^{b} f(x) \mathrm dx$$

Propriétés de comparaison

Positivité : $f(x) > 0$ sur $[a ; b] \Rightarrow \int_{a}^{b} f(x) \mathrm dx > 0$

Croissance : $f(x) > g(x)$ sur $[a ; b] \Rightarrow \int_{a}^{b} f(x) \mathrm dx > \int_{a}^{b} g(x) \mathrm dx$

Intégration par parties

Soit $f$ et $g$ deux fonctions continues et dérivables sur $[a ; b]$ ($a < b$). On suppose que les fonctions dérivées de $f$ et $g$ sont continues sur $[a ; b]$.

On a la formule d'intégration par parties :

$$\int_a^b f(x) g'(x) \mathrm{d}x = [f(x)\times g(x)]_a^b - \int_a^b g(x) f'(x) \mathrm{d}x$$

Calcul d'aire avec l'intégrale définie

Soit $f$ une fonction positive et continue sur l'intervalle $[a~ ; b]$. L'aire de la surface délimitée par la courbe représentative de $f$, l'axe des abscisses et les droites d'équation $x = a$ et $x = b$ est $\displaystyle \int_{a}^{b} f(x) \mathrm dx$ (en unités d'aire).

Application pratique

Pour la fonction $f$ définie par $f(x) = 2{x}^2$ qui est continue et positive sur l'intervalle $[0~; 2]$, l'aire de la surface délimitée par la courbe représentative de $f$, l'axe des abscisses et les droites d'équation $x = 0$ et $x = 2$ est :

$\displaystyle \mathrm A = \int_0^2 f(x) \mathrm dx = \frac{16}{3} \rm ~u.a.$

Valeur moyenne d'une fonction continue

Soit $\mu$ la valeur moyenne d'une fonction $f$ continue sur l'intervalle $[a ; b]$ ($a < b$).

Formule de la valeur moyenne

On a :

$$\mu = \frac{1}{b - a} \int_{a}^{b} f(x) \mathrm dx$$

Application pratique

La valeur moyenne de la fonction $f$ définie par $f(x) = 2x^2$ sur l'intervalle $[0 ; 2]$ est :

$$\mu = \frac{1}{2-0} \int_0^2 f(x) \mathrm dx = \frac{1}{2} \times \frac{16}{3} = \frac{8}{3}$$