L’énergie électrique et puissance en régime sinusoïdal

Allure de la tension : $\bf u(t) = U_M \cdot \sin (\omega t)$

$\bf U_M$ est l’amplitude maximale.

$\bf T$ est la période de tension (en seconde), $f = \dfrac{1}{\rm T}$ est sa fréquence (en Hertz).

$\bf \omega = 2\pi \textit f$ est la pulsation (ou la vitesse angulaire), elle s’exprime en radians par seconde $\rm (rd/s)$.

Et valeur efficace : $\boxed{\rm U = \dfrac{U_M}{\sqrt 2}}$

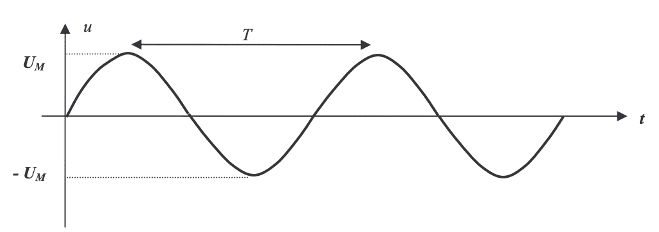
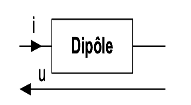
Lorsqu’un dipôle linéaire est soumis à une tension $\rm u$ sinusoïdale, le courant $\rm i$ qui le traverse est lui aussi sinusoïdale.

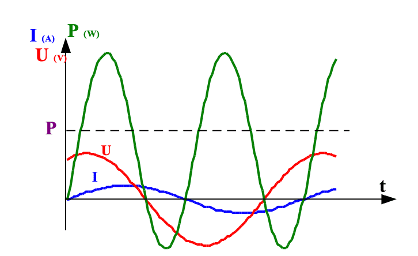
Puissance instantanée :

$\bf p(t) = u(t) \cdot i (t)$

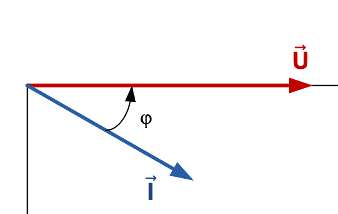
Le courant en retard d’un angle de déphasage $\varphi$.

Puissance active :

La puissance active est la valeur moyenne de la puissance instantanée. Notée $\rm P$ elle s’exprime en WATTS $\rm (W)$. Elle dépend des valeurs efficaces de $\rm u$ et de $\rm i$ et du déphasage $\varphi$ entre les deux grandeurs.

La puissance active reçue par un dipôle se calcule par la relation :

$\boxed{\rm P = U~I\cos\varphi}$ avec $\bf U$ en volts, $\bf I$ en ampères, $\bf P$ en Watts.

Puissance apparente :

Donc la puissance apparente $\bf S$ reçue par un dipôle est égale au produit :

$\boxed{\bf S = U~I}$

L’unité est le VOLTAMPERE : $\bf VA$

Facteur de puissance : 

Le facteur de puissance est le rapport entre la puissance active et apparente. Il est égal au cosinus de l’angle de déphasage $\varphi$.

$\boxed{\bf \cos \varphi = \dfrac{P}{S}}$