Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Les lois de Newton
1ère loi de Newton : Principe d'inertie
Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme si les forces qui s'exercent sur lui se compensent (l'« état » du corps dépend des conditions initiales).
2e loi de Newton : Principe fondamental de la dynamique
Cette loi établit la relation fondamentale entre les forces appliquées à un corps et son accélération.
$$\boxed{\displaystyle \rm \sum \overrightarrow{F_{ext}} = m\vec{\mathcal a}}$$3e loi de Newton : Principe d'action réaction
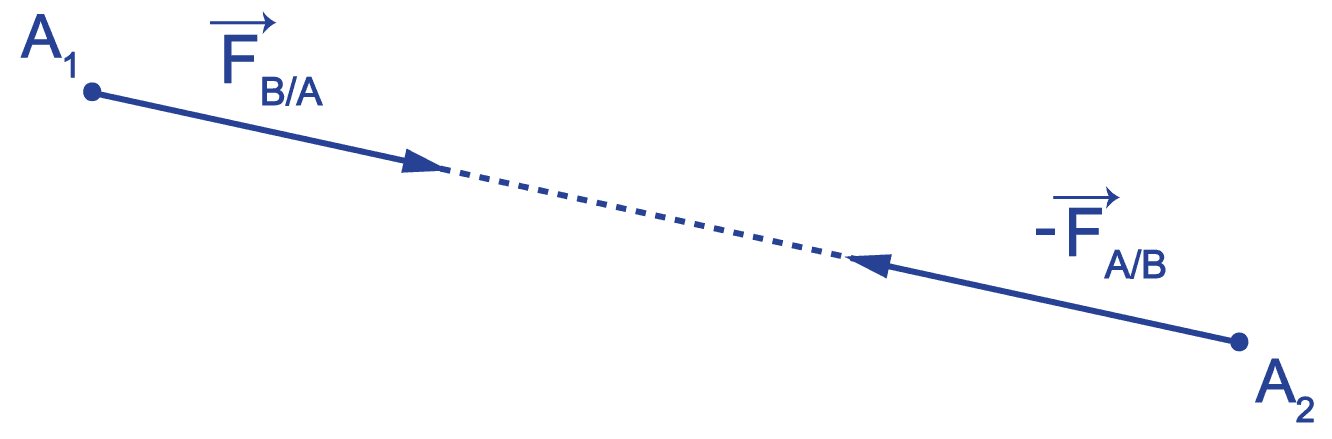
Si un corps $\rm A$ exerce sur un corps $\rm B$ une force $\rm \overrightarrow{F}_{A/B}$, alors $\rm B$ exerce sur $\rm A$ une force $\rm \overrightarrow{F}_{B/A}$ telle que :
$$\rm \overrightarrow{F}_{A/B} = \overrightarrow{-F}_{B/A}$$Que les actions mécaniques entre $\bf A$ et $\bf B$ soient de contact ou à distance, que ces corps soient en mouvement ou immobiles, ces deux forces ont la même direction d'action : la droite $\rm (AB)$ ; la même intensité $\rm (F_{A/B} = F_{B/A})$ mais des sens opposés.
Mouvement dans un champ de pesanteur uniforme
Définition du système d'étude
Système : balle de masse $\rm m$
Référentiel : terrestre supposé galiléen
Bilan des forces : poids de la balle
Application de la 2e loi de Newton
- $\displaystyle \rm \sum \overrightarrow{F_{ext}} = m\cdot \overrightarrow{\mathcal{a(t)}}$
- $\rm \vec P = m\cdot \overrightarrow{\mathcal{a(t)}}$
- $\mathrm m \cdot \vec g = \mathrm m\cdot \overrightarrow{a(t)}$
- $\overrightarrow{a(t)} = \vec g = \overrightarrow{\rm cte}$
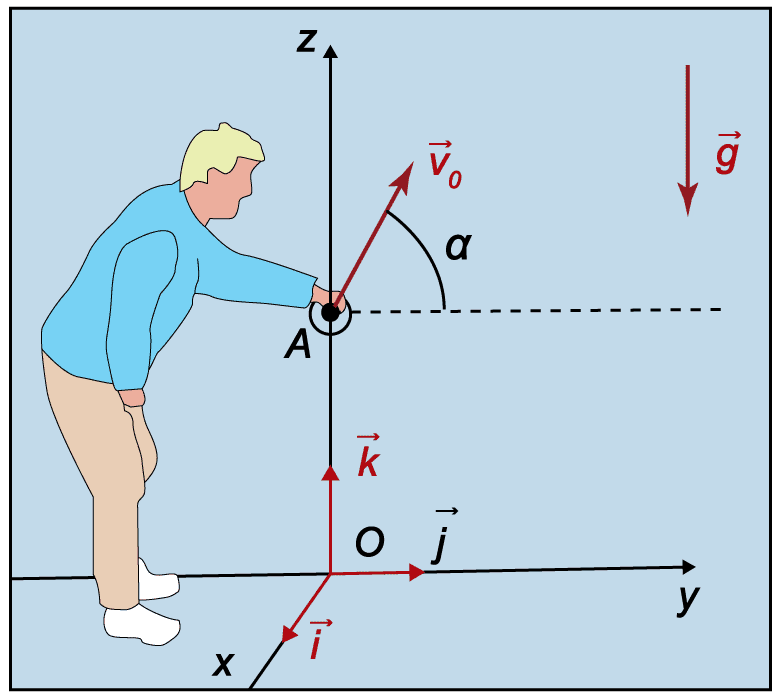
Projection sur les trois axes
On projette sur les 3 axes pour analyser le mouvement dans chaque direction.
Sur Ox--------$\scriptstyle a_x = 0$--------D'où en primitivant : $\scriptstyle v_x = \rm cste_1$
|
Sur Oy--------$\scriptstyle a_y = 0$--------D'où en primitivant : $\scriptstyle v_y = \rm cste_2$
|
Sur Oz--------$\scriptstyle a_z = -g$--------D'où en primitivant : $\scriptstyle v_z = -g \times t + \rm cste_3$
|
Équation de la trajectoire
Grâce à ces deux équations, on peut obtenir l'équation de la trajectoire : $(1)$ Nous donne $t = \dfrac{y}{v_0\times \cos \alpha}$.
On remplace dans $(2)$ :
$$\boxed{ z(y) = -1/2 \times g \times \frac{y^2}{v_0^2 \times \cos^2 \alpha} + \tan \alpha \times y + \rm OA}$$
