Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Les lois de Kepler
Première loi
Dans le référentiel héliocentrique, le centre de chaque planète décrit une trajectoire elliptique dont le Soleil S est l'un des foyers.
Deuxième loi
Le rayon SM qui relie la planète M au Soleil S balaie des aires égales en des temps égaux.
Troisième loi
$$\dfrac{\rm T^2}{a^3} = \dfrac{4\pi^2}{\rm G.M_S}$$
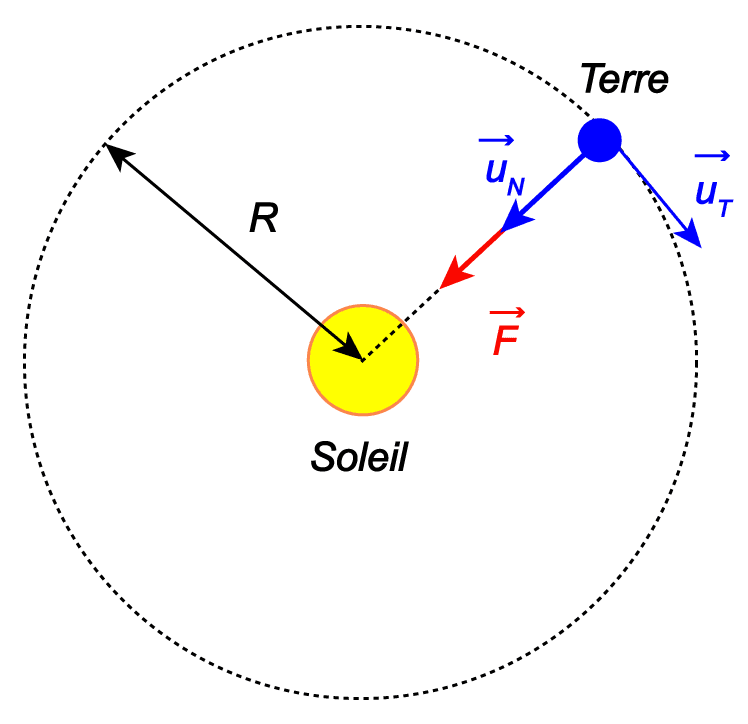
Mouvement circulaire uniforme de la Terre autour du Soleil
Définition du système d'étude
Système : Terre de masse $\rm M_T$
Référentiel : héliocentrique supposé galiléen
Bilan des forces
$$\boxed{\rm \overrightarrow F = G\dfrac{M_TM_S}{R^2}\overrightarrow{\mathcal u_N}}$$ $\left | \begin{array}{lll} \text{F en N}\\ \text{M en kg}\\ \text{R en m}\\ \rm G = 6,67 \cdot 10^{-11}~S.I.\end{array}\right.$
Application de la deuxième loi de Newton
Deuxième Loi de Newton : $\rm \sum \overrightarrow F = \overrightarrow F = M_T \cdot \mathcal{\overrightarrow a}$
$\rm \overrightarrow F = M_T \cdot \mathcal{\overrightarrow a} \Leftrightarrow \dfrac{G.M_TM_S}{R^2}\overrightarrow{\mathcal u_N}$ $\rm = M_T(\mathcal a_T\overrightarrow{\mathcal u_T} + \mathcal a_N\overrightarrow{\mathcal u_N})$ $\rm \Leftrightarrow \dfrac{G.M_T.M_S}{R^2}\overrightarrow{\mathcal u_N}$ $= \rm M_T\mathcal a_T\overrightarrow{\mathcal u_T} + M_T\mathcal a_N\overrightarrow{\mathcal u_N}$
Identification des composantes
Donc, par identification : $\left\{\begin{array}{lll}\rm M_T.\mathcal a_N = \dfrac{G.M_T.M_S}{R^2}\\ \rm \mathcal a_T = 0\end{array}\right.$ $\Leftrightarrow$ $\left\{\begin{array}{ll}a_{\rm N} \rm = \dfrac{G.M_S}{R^2}\\a_{\rm T} = 0\end{array}\right.$
Conséquences du mouvement
Or si $a_T = 0$ alors $\dfrac{\mathrm dv}{\mathrm dt} = 0$ car par définition $a_T = \dfrac{\mathrm dv}{\mathrm dt}$.
Comme $\dfrac{\mathrm dv}{\mathrm dt} = 0$ alors la norme de la vitesse est constante.
Ainsi, si la trajectoire d'un objet en orbite gravitationnelle est circulaire alors son mouvement est uniforme.
Expression de la vitesse orbitale
Comme $a_{\rm N} = \dfrac{v^2}{\rm R}$, on a donc $\dfrac{v^2}{\rm R} = \rm \dfrac{G.M_S}{R^2}$ $\Leftrightarrow$ $$\boxed{v = \rm\sqrt{\dfrac{G.M_S}{R}}}$$ $\left| \begin{array}{lll}v \text{ en } \rm m.s^{-1}\\\rm M_S \text{ en kg}\\ \text{R en m}\\ \rm G = 6,67\cdot 10^{-11}~S.I.\end{array}\right.$
Période de révolution
La période de révolution $\rm T$ est le temps nécessaire à l'objet (ici la Terre) pour faire un tour sur son orbite. La longueur $\rm L$ d'une orbite est égale au périmètre du cercle, soit : $\rm L = 2 \pi R$
Donc $v = \dfrac{\rm L}{\Delta t} = \rm \dfrac{2\pi R}{T}$ donc $\rm T = 2\pi \sqrt{\dfrac{R^3}{GM_S}}$ en utilisant l'expression de $v$ trouvée précédemment.
