La forme de la Terre

Dès l’Antiquité, les observations d’Aristote ont permis de conclure que la Terre était sphérique. Elle apparaît plane dans la plupart des expériences quotidiennes. 

Erathostène, au IIIe siècle avant J-C, détermine la circonférence de la Terre $\bf (40~000~km)$ et son rayon $\bf (6~370~km)$.

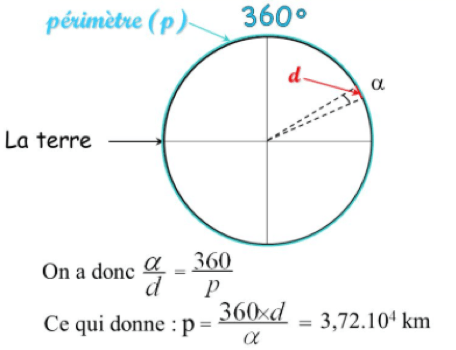
Le périmètre d’un cercle est donné par la relation : $\rm P = 2 \times \pi  \times R$ avec $\bf R$ rayon du cercle en mètre $\bf m$. Le rayon de la Terre avec $\rm R = \displaystyle \frac{40~000}{2 \times \pi} = 6~370~km$.

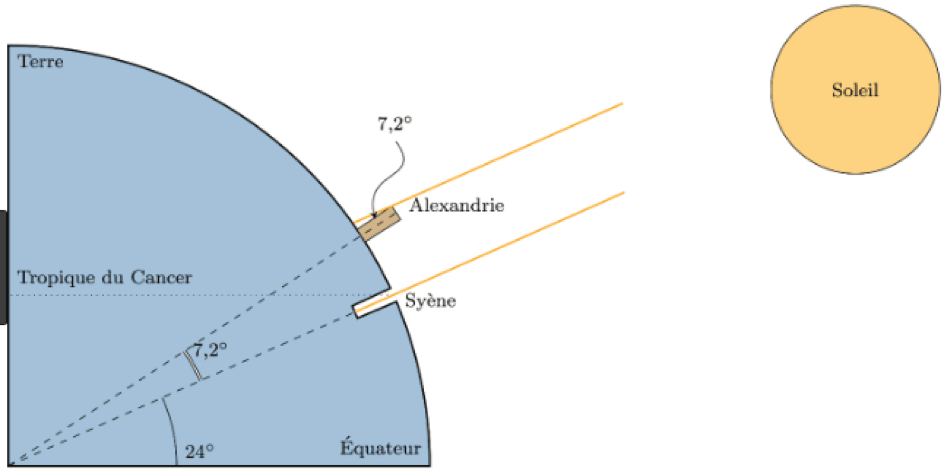
Avec $d = 790~\rm km$ distance séparant Alexandrie de Syène et $\alpha = 7,2°$

Après la révolution, Delambre et Méchain évaluent, par la méthode de triangulation, la distance d’un point inconnu par rapport à deux autres points dont on connaît celle qui les séparent. Le point dont cette distance est inconnue est considéré comme un des sommets du triangle. 

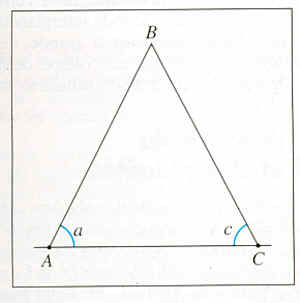
Dans le triangle $\rm ABC$, le point étudié est le point $\rm B$. Nous connaissons $\rm AB$, ainsi que les angles $a$ et $c$.
Il est simple de calculer l’angle $b$, sachant que la somme des sommets d’un triangle est égale à $180°$, il suffit de faire $180-(a+c)$.
La loi des sinus est appliquée :

$$\displaystyle \frac{\rm AC}{\sin b} = \frac{\rm AB}{\sin c} = \frac{\rm BC}{\sin \alpha}$$

Grâce à deux produits en croix, nous connaissons les distances $\rm AB$ et $\rm BC$.

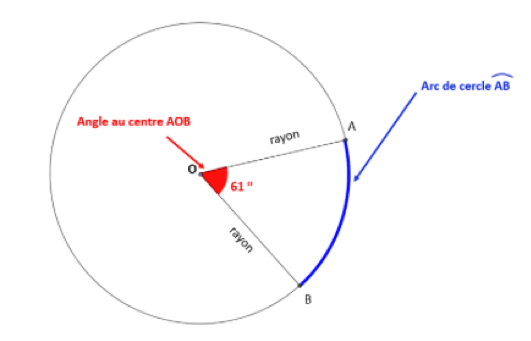
Des coordonnées angulaires permettent de repérer un point à la surface de la Terre : sa latitude et sa longitude. Elles sont exprimées en degrés et mesurées respectivement par rapport à l’Equateur et au méridien origine de Greenwich. La Terre étant de forme sphérique, le plus court chemin entre deux points à sa surface est l’arc du grand cercle qui les relie.

$$\displaystyle\frac{\text{angle au centre}}{360°} = \frac{\text{arc de cercle}}{\text{circonférence}}$$