Exercices par compétences

Dans le cadre d’un problème de dénombrement, utiliser une représentation adaptée et reconnaître les objets à dénombrer

Effectuer des dénombrements simples

Représenter des combinaisons linéaires de vecteurs donnés

Exploiter une figure pour exprimer un vecteur comme combinaison linéaire de vecteurs

Décrire la position relative de deux droites, d’une droite et d’un plan, de deux plans

Lire sur une figure si trois vecteurs de l’espace forment une base et lire la décomposition d’un vecteur dans une base

Étudier géométriquement des problèmes simples de configurations dans l’espace

Utiliser le produit scalaire pour démontrer une orthogonalité, pour calculer un angle, une longueur dans l’espace

Étudier des problèmes de configuration dans l’espace : orthogonalité de deux droites, d’une droite et d’un plan lieux géométriques simples

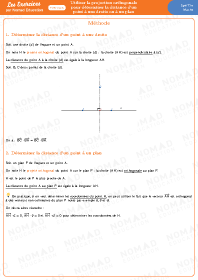
Utiliser la projection orthogonale pour déterminer la distance d’un point à une droite ou à un plan

Déterminer une représentation paramétrique d’une droite / Reconnaître une droite donnée par une représentation paramétrique

Déterminer l’équation cartésienne d’un plan dont on connaît un vecteur normal et un point / Reconnaître un plan donné par une équation cartésienne et préciser un vecteur normal à ce plan

Déterminer les coordonnées du projeté orthogonal d’un point sur un plan donné par une équation cartésienne ou sur une droite donnée par un point et un vecteur directeur

Traduire par un système d’équations linéaires des problèmes : étudier une configuration dans l’espace

Établir la convergence d’une suite ou sa divergence vers +∞ ou –∞

Raisonner par récurrence pour établir une propriété d’une suite

Déterminer la limite d’une fonction en un point, en ±∞

Faire le lien entre l’existence d’une asymptote parallèle à un axe et celle de la limite correspondante

Calculer la dérivée d’une fonction donnée par une formule simple

Calculer la fonction dérivée, déterminer les limites et étudier les variations d’une fonction

Lire sur une représentation graphique de 𝑓, de 𝑓’ ou de 𝑓’’ les intervalles où 𝑓 est convexe, concave et les points d’inflexion

Esquisser l’allure de la courbe représentative d’une fonction 𝑓 à partir de la donnée de tableaux de variations de 𝑓, de 𝑓’ ou de 𝑓’’

Démontrer des inégalités en utilisant la convexité d’une fonction

Étudier les solutions d’une équation du type 𝑓(𝑥) = 𝑘 : existence, unicité, encadrement

Pour une fonction continue 𝑓 d’un intervalle dans lui-même, étudier une suite définie par une relation de récurrence 𝑢_{𝑛+1} = 𝑓(𝑢_𝑛)

Utiliser l’équation fonctionnelle de l’exponentielle ou du logarithme pour transformer une écriture, résoudre une équation, une inéquation

Dans le cadre d’une résolution de problèmes, utiliser les propriétés des fonctions exponentielle et logarithme

Savoir résoudre une équation du type cos(𝑥) = 𝑎, une inéquation de la forme cos(𝑥) ⩽ 𝑎 sur [-π, π]

Étudier une fonction simple, définie à partir de fonction trigonométrique, pour déterminer des variations, un optimum

Calculer une primitive en utilisant les primitives de référence et les fonctions de la forme (𝑣’ ∘ 𝑢) × 𝑢’

Pour une équation différentielle 𝑦’ = 𝑎𝑦 + 𝑏, (𝑎 ≥ 0) : déterminer une solution particulière constante, utiliser cette solution pour déterminer toutes les solutions

Pour une équation différentielle 𝑦’ = 𝑎𝑦 + 𝑓 : à partir de la donnée d’une solution particulière, déterminer toutes les solutions

Estimer graphiquement ou encadrer une intégrale, une valeur moyenne

Calculer une intégrale à l’aide d’une primitive à l’aide d’une intégration par parties

Majorer (minorer) une intégrale à partir d’une majoration (minoration) d’une fonction par une autre fonction

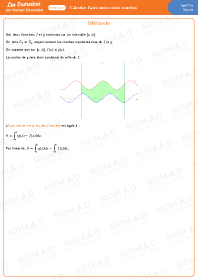
Calculer l’aire entre deux courbes

Étudier une suite d’intégrales, vérifiant éventuellement une relation de récurrence

Interpréter une intégrale, une valeur moyenne

Modéliser une situation par une succession d’épreuves et la représenter par un arbre, puis calculer des probabilités

Modéliser une situation par un schéma de Bernoulli, par une loi binomiale

Utiliser l’expression de la loi binomiale pour calculer des probabilités

Chercher des valeurs pour qu’une probabilité soit inférieure ou supérieure à une valeur donnée

Représenter une variable comme somme de variables aléatoires plus simples

Calculer l’espérance d’une variable aléatoire

Calculer la variance d’une variable aléatoire

Appliquer l’inégalité de Bienaymé-Tchebychev pour définir une taille d’échantillon, en fonction de la précision et du risque choisi