Résoudre des problèmes multiplicatifs simples

Pour résoudre ce genre de problème, il faut bien comprendre ce que l'on cherche.

J'observe les données. Je m'interroge : ai-je « une part », « le nombre de parts » ou « le tout » ?

Je peux représenter ma recherche à l'aide d'une représentation en barre de ce type :

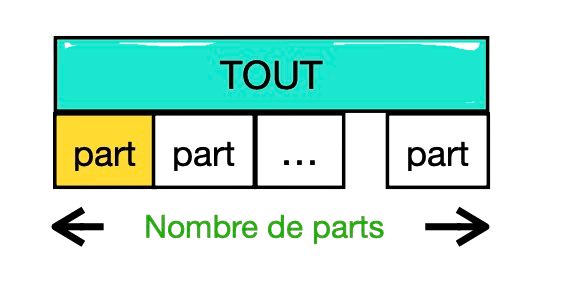
Recherche du tout

Dans ce problème, j'ai « une part » : pour un collier, Emma utilise 24 perles, et « le nombre de parts » : Emma réalise 30 colliers.

Je cherche donc « le tout » : combien de perles au total.

Je calcule $24 \times 30 = 720$

Je rédige ma phrase réponse : « Emma a utilisé 720 perles. »

Recherche d'une part

Dans ce problème, j'ai « le tout » : 360 perles au total, et « le nombre de parts » : Emma a réalisé 9 colliers.

Je cherche donc combien vaut « une part » : $9 \times ? = 360$.

Je calcule $9 \times 40 = 360$

Je rédige ma phrase réponse : « Un collier contient 40 perles. »

Recherche du nombre de parts

Dans ce problème, j'ai « le tout » : 560 perles au total, et ce que vaut « une part » : un collier contient 70 perles.

Je cherche donc « le nombre de parts » : $? \times 70 = 560$.

Je calcule $8 \times 70 = 560$

Je rédige ma phrase réponse : « Emma a réalisé 8 colliers. »