Résoudre des problèmes additifs simples

Pour résoudre ce problème, il faut bien comprendre ce que l'on cherche.

J'observe les données. Je m'interroge : ai-je « une partie », « un tout » ?

Je peux représenter ma recherche à l'aide de cette représentation :

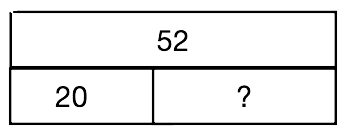
Dans ce problème, j'ai « une partie » : $20$ qui correspond à ce que Lucas donne et « un tout » : $52$ qui correspond à la collection totale au départ.

Je cherche combien pour aller de $20$ à $52$.

Je calcule $52 - 20 = 32$

Je rédige ma phrase réponse : « Il lui reste 32 images. »

Voici un autre exemple utilisant la comparaison

Je compare les 2 quantités : le nombre d'élèves de chaque école. J'ai le nombre total d'élèves de l'école Pasteur.

⚠️ : le vocabulaire de l'énoncé peut t'induire en erreur. Il est écrit « de plus qu'.. » alors qu'il faut effectuer une soustraction. Dire qu'il y a $72$ élèves de plus à l'école Pasteur qu'à l'école Picasso revient à dire qu'il y a $72$ élèves de moins à l'école Picasso qu'à l'école Pasteur.

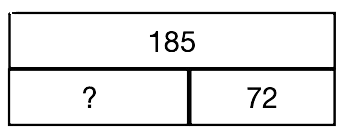
$185 - 72 = 113$

Il y a 113 élèves à l'école Picasso.