Fractions supérieures à 1

Qu'est-ce qu'une fraction supérieure à 1 ?

Une fraction supérieure à 1 représente plus d'une unité.

Exemples 

Si l'unité est un rectangle

$\displaystyle \frac{5}{2} > 1$

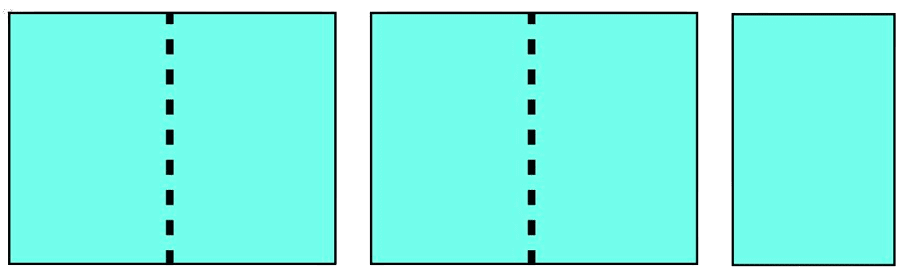
Pour représenter $\displaystyle \frac{5}{2}$, on utilise 2 rectangles entiers et un demi rectangle.

Si l'unité est un disque

$\displaystyle \frac{13}{4} > 1$

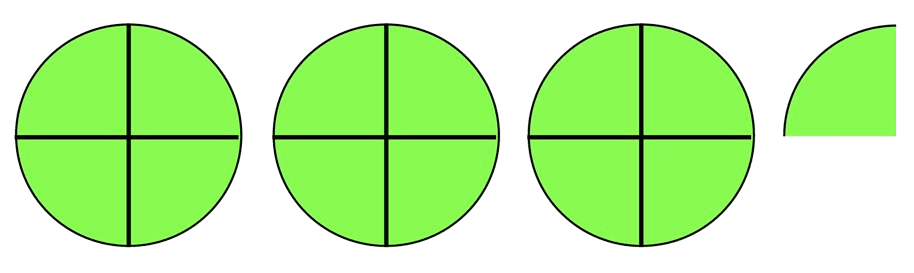
Pour représenter $\displaystyle \frac{13}{4}$, on utilise 3 cercles entiers entiers et un quart de cercle.

Remarque : quand une fraction est plus grande que 1, le numérateur (nombre du haut) est plus grand que le dénominateur (nombre du bas).

Écrire une fraction comme une somme d'un entier et d'une fraction

Quand une fraction est supérieure à 1, on peut l'écrire comme une somme. On cherche le maximum d'unité et on ajoute le reste (plus petit que 1).

Reprenons nos deux exemples :

$\displaystyle \frac{5}{2} = \frac{2}{2} + \frac{2}{2} + \frac{1}{2} = 1 + 1 + \frac{1}{2} = 2 + \frac{1}{2}$ (2 rectangles et un demi rectangle)

$\displaystyle \frac{13}{4} = \frac{4}{4} + \frac{4}{4} + \frac{4}{4} + \frac{1}{4} = 1 + 1 + 1 + \frac{1}{4} = 3 + \frac{1}{4}$ (3 cercles et $\frac{1}{4}$ de cercles)

Transformer une somme en une seule fraction

On peut aussi faire l'inverse :

$2 + \displaystyle \frac{1}{3} = \left(\frac{3}{3} + \frac{3}{3}\right) + \frac{1}{3} = \frac{7}{3}$

On transforme les 2 unités en $\displaystyle \frac{6}{3}$ car 1 unité vaut $\displaystyle \frac{3}{3}$.

Autres exemples :

$1 + \displaystyle \frac{3}{4} = \frac{4}{4} + \frac{3}{4} = \frac{7}{4}$

$2 + \displaystyle \frac{7}{10} = \frac{10}{10} + \frac{10}{10} + \frac{7}{10} = \frac{27}{10}$