Fractions et nombres décimaux

Lire et comprendre les nombres décimaux

$9,07$ → $9$ unités et $7$ centièmes → $9 + \dfrac{7}{100}$

$541,86$ → $5$ centaines, $4$ dizaines, $1$ unité, $8$ dixièmes et $6$ centièmes → $500 + 40 + 1 + \dfrac{8}{10} + \dfrac{6}{100}$

$0,409$ → $4$ dixièmes et $9$ millièmes → $\dfrac{4}{10} + \dfrac{9}{1000}$

Tu peux t'aider d'un tableau :

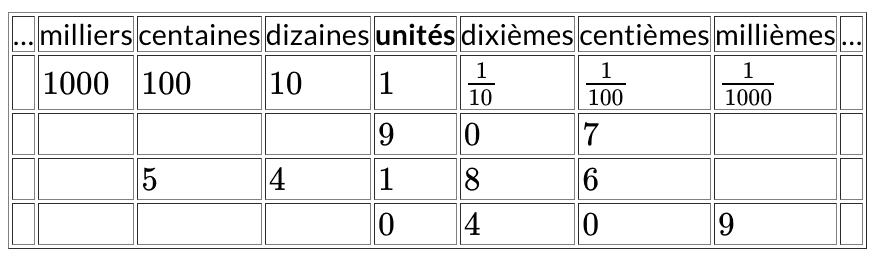
Pour lire le nombre $541,86$ :

• tu peux dire la partie décimale en une seule fois → $541$ unités et $86$ centièmes
• Tu peux décomposer la partie décimale → $541$ unités, $8$ dixièmes et $6$ centièmes

Pour lire le nombre $0,409$ :

• tu peux dire la partie décimale en une seule fois → $409$ millièmes
• Tu peux décomposer la partie décimale → $4$ dixièmes et $9$ millièmes

Passer d'une écriture à l'autre

$7,2 = 7 + \dfrac{2}{10}$

$87,09 = 87 + \dfrac{9}{100}$

$6,87 = 6 + \dfrac{87}{100} = 6 + \dfrac{8}{10} + \dfrac{7}{100}$

$\dfrac{5}{10} + \dfrac{4}{1000} = 0,504$

$94 + \dfrac{5}{100} = 94,05$

$\dfrac{8}{10} + 23 + \dfrac{5}{100} + \dfrac{1}{1000} = 23,851$

Rappelle-toi que :

• les dixièmes sont à la première place après la virgule,
• Les centièmes sont à la deuxième place après la virgule,
• Les millièmes sont à la troisième place après la virgule…