Encadrer une fraction par deux entiers consécutifs

Encadrer une fraction par deux nombres entiers consécutifs, c'est trouver deux nombres qui se suivent entre lesquels elle se trouve.

`Exemple`

$\displaystyle \frac{13}{4}$ est entre $3$ et $4$,

$3 < \displaystyle \frac{13}{4} < 4$

Pour trouver cet encadrement, tu peux utiliser la décomposition pour savoir combien d'unités tu peux faire :

$\displaystyle \frac{13}{4} = 3 + \frac{1}{4}$

Dans $1$ unité, il y a $\frac{4}{4}$ donc dans $3$ unités, il y a $\displaystyle \frac{12}{4}$. Il reste $\displaystyle \frac{1}{4}$ pour faire $\displaystyle \frac{13}{4}$.

$\displaystyle \frac{1}{4}$ est plus petit que $1$.

$\displaystyle \frac{13}{4}$ est donc plus grand que $3$ unités et plus petit que $4$ unités.

Tu peux aussi utiliser un schéma pour t'aider :

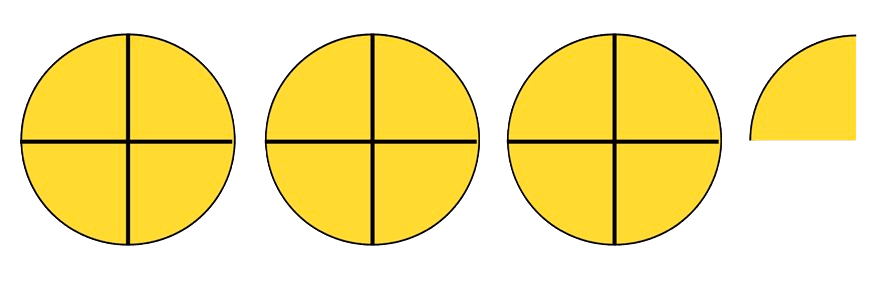
Ce schéma montre qu'il y a plus de $3$ cercles ($3$ entiers et $\displaystyle \frac{1}{4}$ de cercle) et moins de $4$ cercles.

`Autres exemples`

$4 < \displaystyle \frac{9}{2} < 5$ car dans une unité, il y a $\dfrac{2}{2}$ ➡️ $\dfrac{9}{2} = 4 + \displaystyle \frac{1}{2}$

$7 < \displaystyle \frac{37}{5} < 8$ car dans une unité, il y a $\displaystyle \frac{5}{5}$ ➡️ $\displaystyle \frac{37}{5} = 7 + \dfrac{2}{5}$

$8 < \displaystyle \frac{85}{10} < 9$ car dans une unité, il y a $\displaystyle \frac{10}{10}$ ➡️ $\displaystyle \frac{85}{10} = 8 + \frac{5}{10}$