Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Pour comparer des fractions qui ont le même dénominateur (c'est-à-dire le même nombre total de parts égales), il faut comparer le numérateur (c'est-à-dire le nombre de parts coloriées).
Exemple
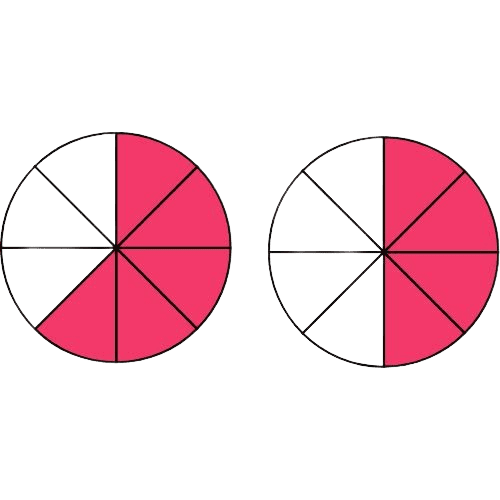
Il y a 5 parts coloriées dans le premier gâteau et 4 parts dans le deuxième. 5 > 4 donc $\displaystyle \frac{5}{8}> \frac{4}{8}$.
Pour comparer des fractions qui ont le même numérateur, il faut comparer le dénominateur.
Exemple
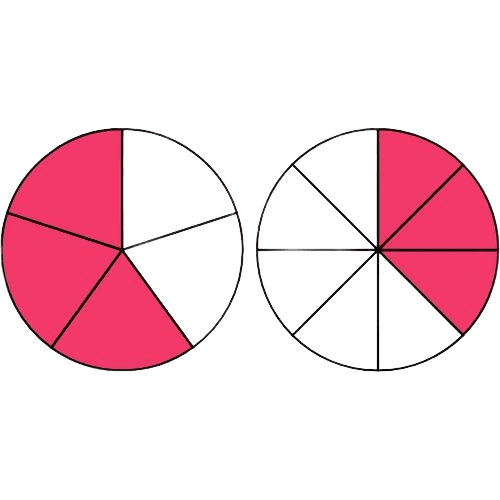
➡️ Plus le dénominateur est grand (8), plus les parts sont petites. Donc $\displaystyle \frac{3}{8} < \frac{3}{5}$.
Pour comparer des fractions qui n'ont pas le même dénominateur, il faut partager la même bande avec différentes parts égales.
Exemple
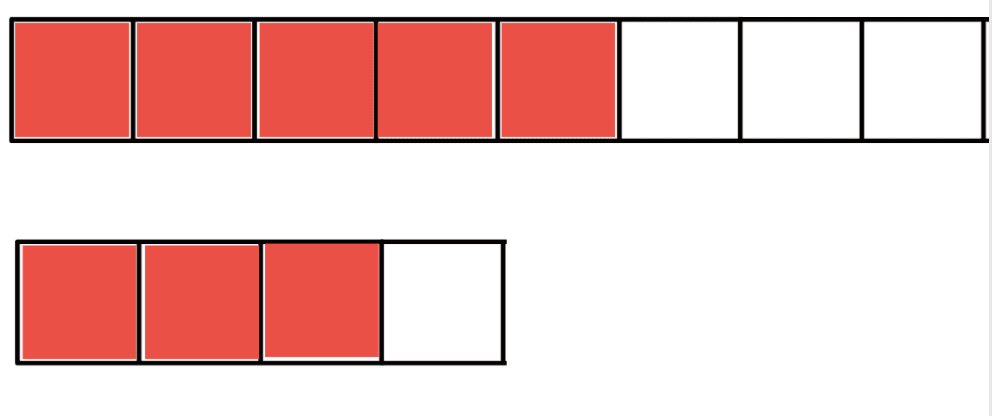
➡️ Les deux bandes font la même taille. La partie coloriée de la deuxième est plus grande que celle de la première bande. Cela veut dire que $\displaystyle \frac{3}{4} > \frac{5}{8}$
➡️ Je sais que pour un même tout, si je fais des parts deux fois plus petites alors je prends deux fois plus de parts. Donc $\displaystyle \frac{3}{4} = \frac{6}{8}$ et donc $\displaystyle \frac{6}{8} > \frac{5}{8}$
