Géométrie

Périmètres des figures usuelles

Aire des figures usuelles

Les triangles usuels et leurs principales propriétés

Les quadrilatères usuels et leurs principales propriétés

Volumes

• Pavé droit (dimensions $a$, $b$ et $c$) : $a \times b \times c$ ;
• Cube (côté $a$) : $a^3$ ;
• Cylindre (rayon de base $\rm R$, hauteur $h$) : $\pi \mathrm R^2 \times h$ ;
• Boule (rayon $\rm R$) : $\displaystyle \frac{4\pi \rm R^3}{3}$.

Théorème de Pythagore 

Dans le triangle $\mathrm{ABC}$ rectangle en $\mathrm{A}$, on a : ${\mathrm{BC}}^2 = {\mathrm{AB}}^2 + {\mathrm{AC}}^2$.

Le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés. 

Application :

Dans un triangle $\mathrm{ABC}$ rectangle en $\mathrm{A}$, on a $\mathrm{AB = 3 \:cm}$ et $\mathrm {BC = 5\: cm}$.

Calculons $\mathrm{AC}$ :

D’après le théorème de Pythagore, on a ${\mathrm{BC}}^2 = {\mathrm{AB}}^2 + {\mathrm{AC}}^2$.
$5^2 = 3^2 + {\mathrm{AC}}^2$ donc ${\mathrm{AC}}^2 = 25 - 9 = 16$, puis $\mathrm{AC = \sqrt{16} = 4 \:cm}$.

Réciproque du théorème de Pythagore 

Dans un triangle $\mathrm{ABC}$, si ${\mathrm{BC}}^2 = {\mathrm{AB}}^2 + {\mathrm{AC}}^2$, alors le triangle est rectangle en $\mathrm A$ et le segment $\mathrm{[BC]}$ est l’hypoténuse de ce triangle rectangle.

Théorème de Thalès

Soient $\rm A$, $\rm M$ et $\rm B$ trois points alignés et $\rm A$, $\rm N$ et $\rm C$ trois autres points alignés dans le même ordre.

On a deux configurations possibles :

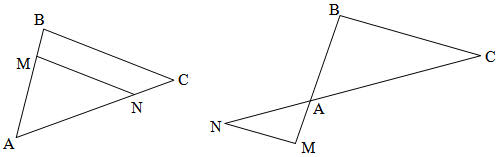
Si les droites $\rm (BC)$ et $\rm (MN)$ sont parallèles, alors on a $\displaystyle \frac{\rm{AM}}{\rm{AB}} = \frac{\rm{AN}}{\rm{AC}} = \frac{\rm{MN}}{\rm{BC}}$.

Objectif

Savoir calculer le périmètre, l'aire ou le volume d'une figure ou d'un solide courant.

Pourquoi c'est important ?

Ces formules sont utiles pour

Objectif

Savoir reconnaître quand utiliser Pythagore et calculer la longueur d'un côté dans un triangle rectangle.

Pourquoi c'est important ?

Objectif

Comprendre et appliquer le théorème de Thalès pour calculer des longueurs dans des triangles avec des droites parallèles.

Pourquoi c'est important&