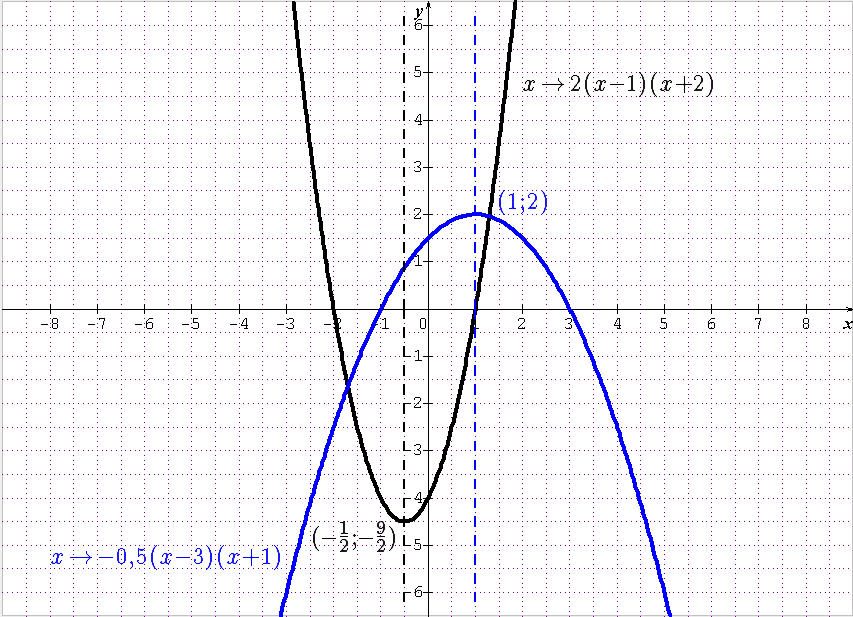
Fonctions $x\mapsto a(x - x_1)(x - x_2)$, $a\neq 0$, $x_1 < x_2$ trois réels
Cas où $a > 0$
Si $a > 0$, la courbe représentative de cette fonction est une parabole orientée vers le haut. Elle coupe l'axe des abscisses en $x = x_1$ et $x = x_2$.
La position de la courbe par rapport à l'axe des abscisses est la suivante :
- Au-dessus de l'axe des abscisses sur les intervalles $]-\infty~;~x_1[$ et $]x_2~;~+\infty[$
- Au-dessous de l'axe des abscisses sur l'intervalle $]x_1~;~x_2[$
Cas où $a < 0$
Si $a < 0$, la courbe représentative de cette fonction est une parabole orientée vers le bas. Elle coupe l'axe des abscisses en $x = x_1$ et $x = x_2$.
La position de la courbe par rapport à l'axe des abscisses est la suivante :
- Au-dessous de l'axe des abscisses sur les intervalles $]-\infty~;~x_1[$ et $]x_2~;~+\infty[$
- Au-dessus de l'axe des abscisses sur l'intervalle $]x_1~;~x_2[$
Propriétés générales
Dans tous les cas, la courbe représentative de cette fonction admet pour extremum le point $\displaystyle \mathrm S\left(\frac{x_1 + x_2}{2} ; \frac{-a{(x_2 - x_1)}^2}{4}\right)$ et pour axe de symétrie la droite d'équation $\displaystyle x = \frac{x_1 + x_2}{2}$.
Exemples de représentations graphiques
 Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
