Wave characteristics

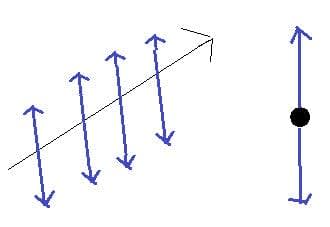
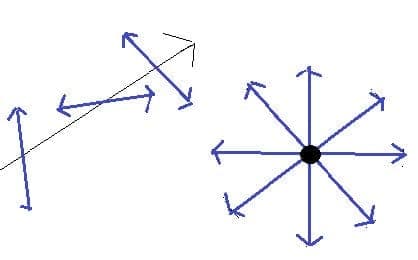
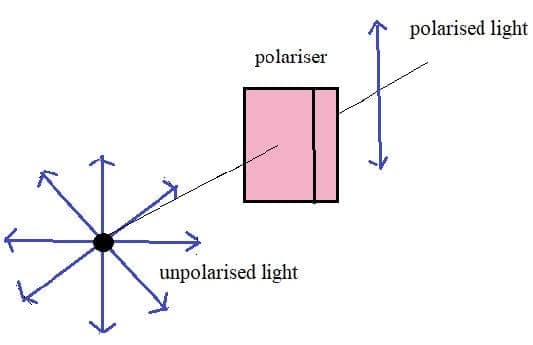
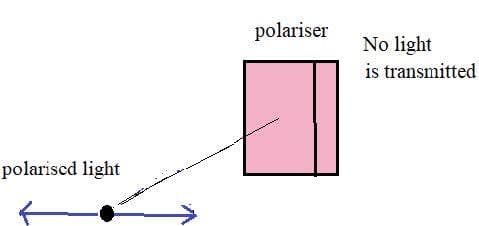
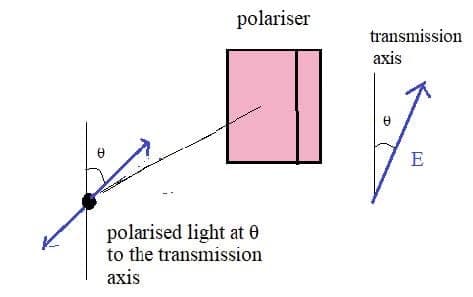
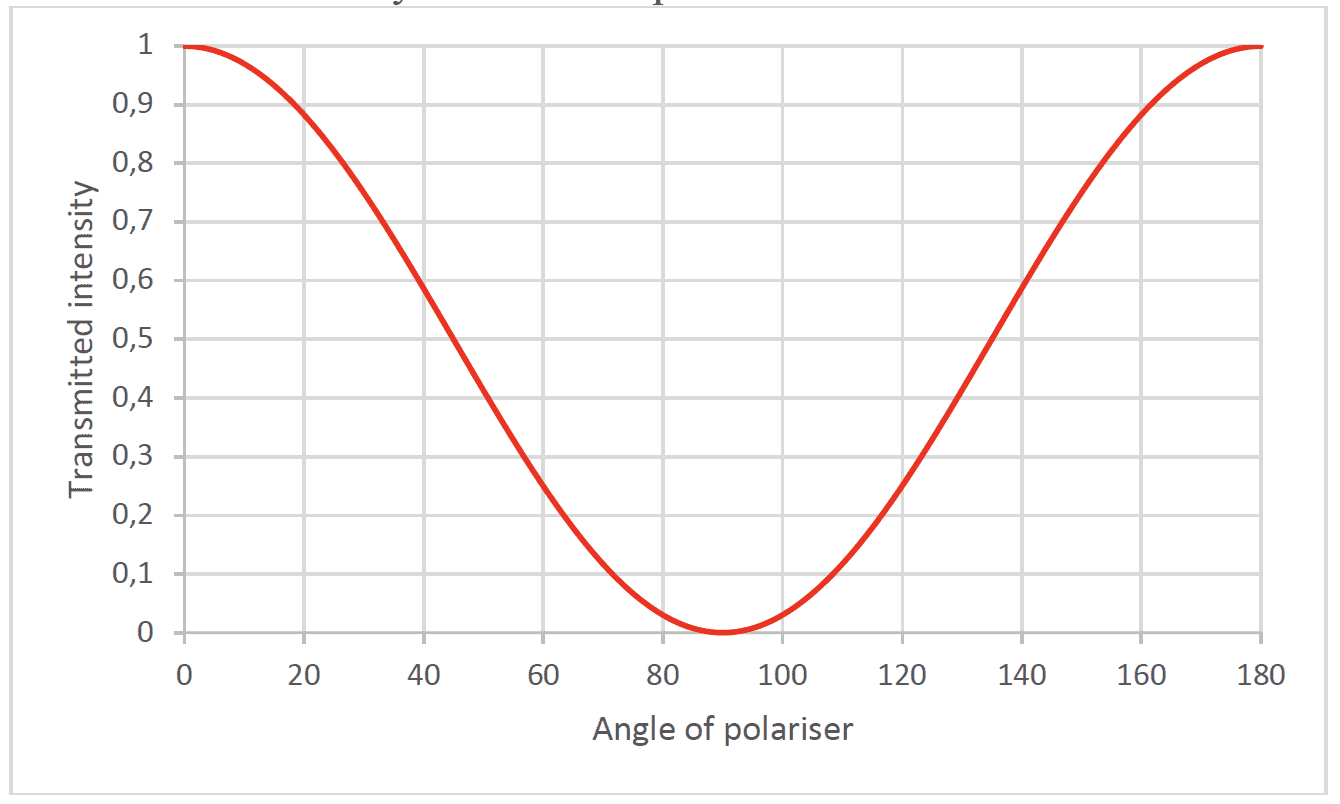
All waves can be described by the same sets of mathematical ideas. Detailed knowledge of one area leads to the possibility of prediction in another.

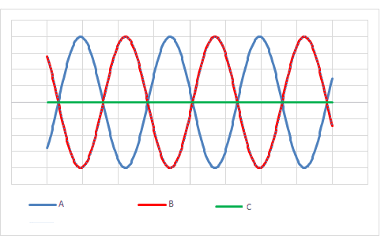
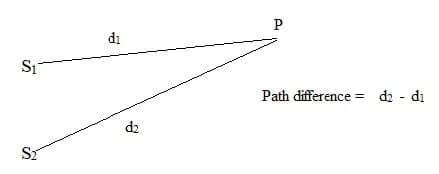
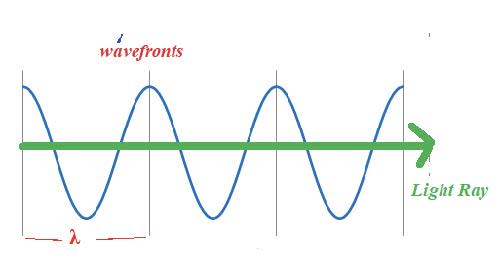
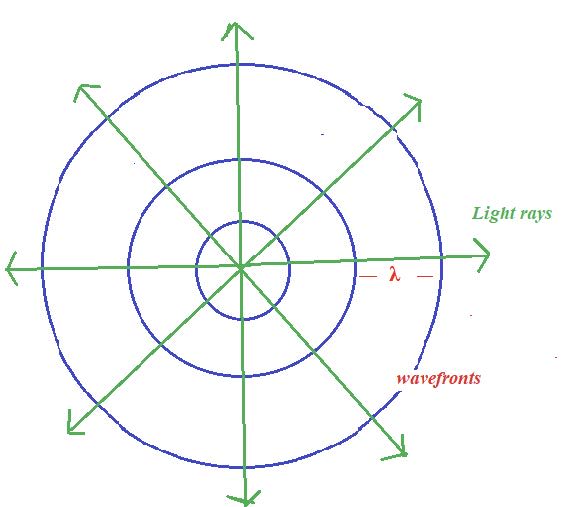
• The direction of energy transfer of a wave can be shown as a ray.
• The wavefronts are at right angles to the rays. All points on a wavefront have the same phase: they are generally shown at the crests and neighbouring wavefronts and are separated by a wavelength.
• Rays and wavefronts are shown for linear and circular waves:
  

• The intensity, $\bf I$, is the power transferred by the wave per unit area: $\rm I = P/A$. The units of $\rm I$ are $\rm Wm^{-2}$.
• The intensity of a wave is proportional to the square of the amplitude, $\rm I \propto A^2$.
  The graph, for example, shows two sound waves of the same pitch/frequency. The red curve corresponds to a note of twice the amplitude of the blue note It has four times the intensity.
  

• If the point source radiates a total power $\rm P$ in all directions, then the intensity I at a distance $\rm R$ away from the point source is:
  $\rm I = P/A$
  Where $\rm A$ is the surface area of a sphere: $\rm 4\pi R^2$
  $\rm I = P/A = P/4\pi R^2$
• A doubling of distance will result in the reduction of the power received to a quarter of the original value.
  $\bf I \propto 1/R^2$
  

• When two waves meet the resultant displacement is the sum of the individual displacements.
• Constructive interference occurs when two waves of the same frequency meet crest to crest to form a wave with an increased amplitude.
  Wave $\rm A$ and Wave $\rm B$ interfere constructively to form wave $\rm C$:
  
• Destructive interference occurs when two waves meet crest to trough, the result is a wave of reduced amplitude.
  
  When the two waves have equal amplitude and frequency. The resulting wave has zero amplitude: there is no wave.
  

• Sources are coherent if the phase difference between the sources is constant.
• If identical waves from two coherent sources arrive at the same point in space they interfere constructively with each other.
• The nature of the interference depends on the difference in the distance the two waves have travelled: the path difference.
• If the path difference between the two rays is a whole number (n) of wavelengths: there is constructive interference.
• If the path difference between the two rays is an odd number of half wavelengths: there is destructive interference.
  

  $\rm (d_{2}-d_{1}) / \lambda=n$: constructive interference $\rm d_{2}-d_{1}) n +1 / 2$: destructive interference

• Light is a transverse wave in which a pair of electric and magnetic fields oscillate, at right angles to each other and the direction of propagation.
• The plane of vibration of electromagnetic waves is defined as the plane that contains the electric field and the direction of propagation.
• There are an infinite number of ways in which the fields can be oriented. Plane-polarized light has a fixed plane of vibration. Unpolarised light has many planes of vibration.
  

  	Polarised light has a fixed plane of vibration.
  	Unpolarised light has many planes of vibration.

• Polarisation is a property of transverse waves only.
• Most visible light sources like the sun and light bulbs produce unpolarized light.
• Radio waves, radar, and microwaves are often plane-polarized.
• Light can be polarised as a result of reflection or selective absorption. Reflected light is polarised parallel to the reflecting surface (see later).
• A polariser is a piece of plastic with a specific transmission axis. Only light with its electric field parallel to the axis is transmitted.
• When unpolarised light is incident on a polariser with a vertical transmission axis. The transmitted light is vertically polarised.
  
• The transmitted intensity is half of the incident intensity: $\rm I = I_0/2$.
• Polarised light with an electric field at right angles to the transmission axis is blocked.
  

• When the electric field is at an angle θ to the transmission axis the component that can be transmitted is $\rm E\cos\theta$.
  $\rm I/ I_0 = E^2 \cos^2\theta / E^2$
  The transmitted intensity is $\rm I = I_0 \cos^2\theta$ a result known as Malus’ law.
  
• The transmitted intensity varies as the polariser is rotated from $0$ to $180°$ as shown:
  
• Note the average value of $\cos^2\theta = ½$ which explains why the transmitted intensity of unpolarised light is half of the incident intensity, $\rm I = I_0/2$.