Wave behaviour

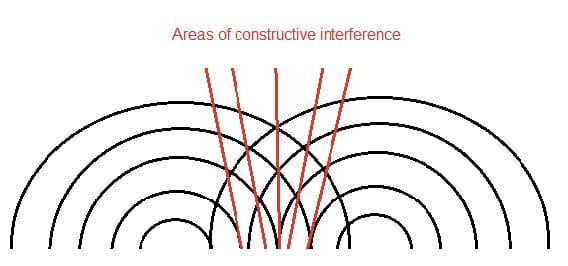
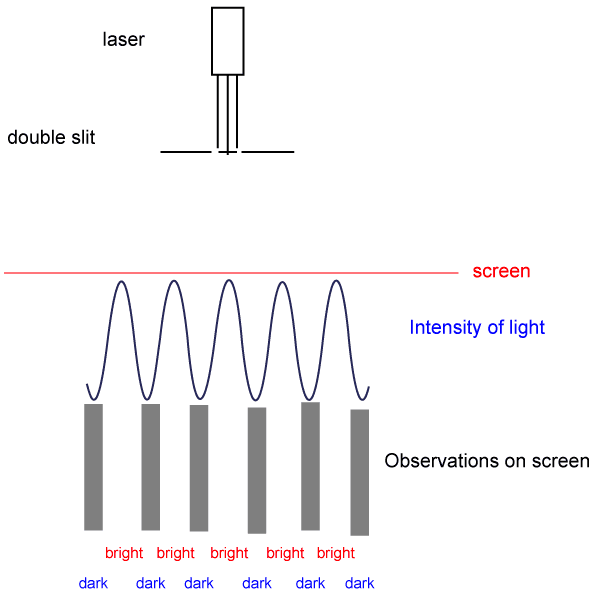
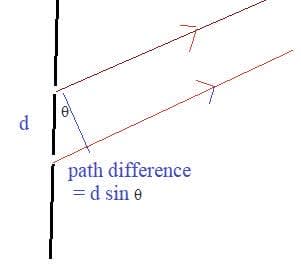
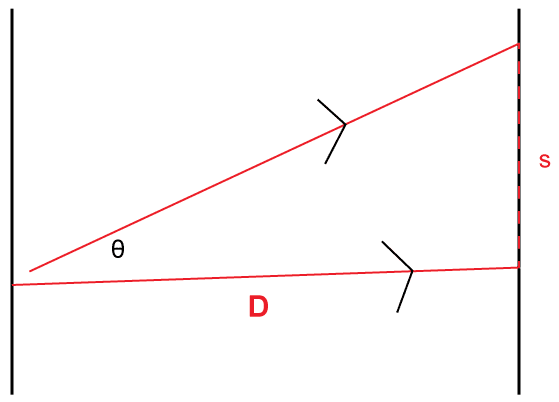
Waves interact with media and each other in a number of ways.

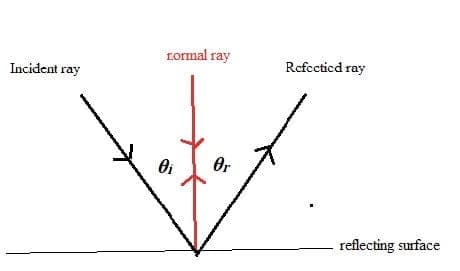
• The normal ray has an angle of incidence of $0^0$. It is the reference for other rays.
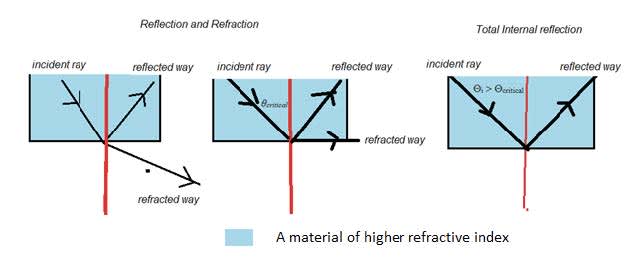
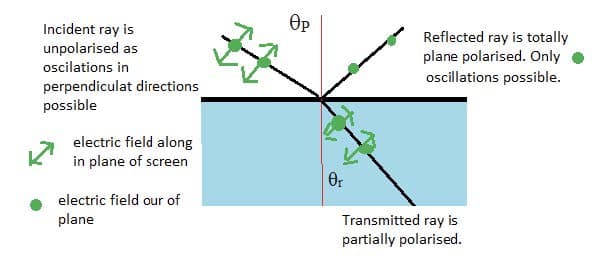
• A wave reflects off a smooth surface. The angle of incidence $\theta_i$ is equal to the angle of reflection $\theta_r$. The incident reflected rays and normal are in the same plane.
  
  
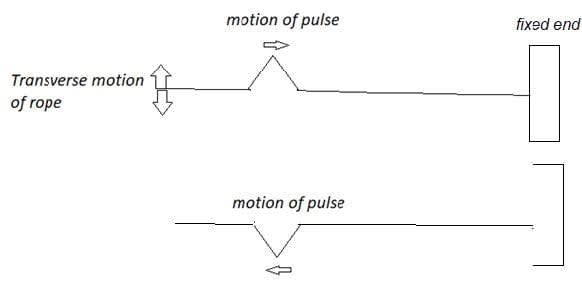
• A pulse travelling along a rope from is reflected at the fixed end. The reflected pulse is inverted.
  
  
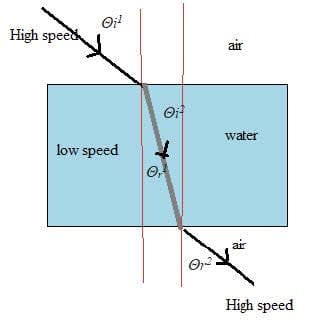
• A wave generally changes speed as it passes from one medium into another. If the speed decreases the ray is bent towards the normal. If the speed increases the ray is bent away from the normal.
• Let $v_{\text {air }}$ and $v_{\text {water }}$ be the speeds of the wave in the two media.
• In the example $\theta _i^{l}>\theta_r^{1}$ as $v_{\text {air }}>v_{\text {water }}$ and $\theta_{i}{ }^{2}<\theta_{\mathrm{r}}{ }^{2}$ as $v_{\text {water }} < v_{\text {air}}$.
  
• Consider the diagram below. In time $\Delta t$ the wavefront has moved $v_{\rm air}$ $\Delta t$ through the air and $v_{\rm water}$ $\Delta t$ through the water.
  
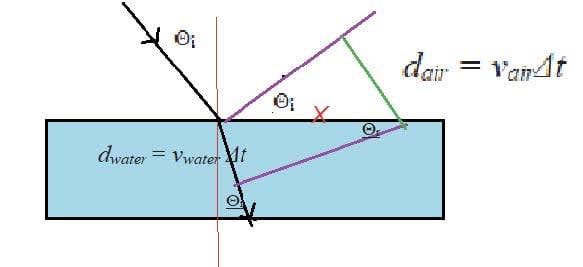
• This gives:
  $\sin \theta_{i}=v_{\text {air }} \Delta t / \mathrm{X}$ $\quad$ $\sin \theta_r = v_{\rm water}\Delta t / \rm X$
  $\sin \theta_{i} / \sin \theta_{r}=(v_{\rm air} \Delta t / X) /(v_{\rm water} \Delta t / \rm X)$
  $\sin \theta_i / \sin \theta_r = v_{\rm air} / v_{\rm water}$
• The speed of light in a medium depends on the refractive index $\boldsymbol{n}$ of the medium:
  $n_{\text {medium }}=c_{\text {vacuum }} / v_{\text {medium }}$
• This leads to $\sin \theta_{1} / \sin \theta_{2}=v_{1} / v_{2}=\mathrm{n}_{2} / \mathrm{n}_{1}$
  $n_{1} \sin \theta_{1}=n_{2} \sin \theta_{2}$
• Water waves refract when they move from deep to shallow water as the speed is reduced in shallow water.
• The frequency of a wave does not change as it passes a boundary from one medium to another.
  $A s v=f \lambda$
  A change in speed corresponds to a change in wavelength.
  The wavelength decreases if the speed decreases and the wavelength increases if the speed increases.

• Reflection occurs at all boundaries between medium of different refraction index.
• When a ray of light enters a medium of lower refractive index, the refracted ray bends away from the normal.
• At the critical angle of incidence, the angle of refraction $= 90^0$.
  
• No refraction takes place for angles of incidence greater than the critical angle. Instead, the ray reflects back into the medium from which it came: total internal reflection.
• The critical angle is related to the refractive index.
  $\sin \theta_{1} / \sin \theta_{2}=n_{2} / n_{1}$
  $\theta_{1}=\theta_{\text {critical }} \theta_{2}=90°$
  $\sin \theta_{\rm critical} / 1=n_{2} / n_{1}$
  $\sin \theta_{\rm critical}=n_{2} / n_{1}$

• Earlier it was stated that an incident ray on the boundary between two media is reflected and refracted. The reflected ray is generally partially plane-polarized.
• The reflected ray is totally plane-polarised when perpendicular to the refracted ray. The angle of incidence for this condition is known as the polarising angle.
  
  $\sin \theta_{\mathrm{p}} / \sin \theta_{\mathrm{r}}=\mathrm{n}$
  $\theta_{\mathrm{r}}=180-90-\theta_{\mathrm{p}}=90-\theta_{\mathrm{p}}$
  $\sin \theta_{\mathrm{p}} / \sin \left(90-\theta_{\mathrm{P}}\right)=\mathrm{n}$
  $\sin \theta_{\mathrm{p}} / \cos \left(\theta_{\mathrm{P}}\right)=\mathrm{n}$
  $\tan \theta_{\mathrm{p}}=\mathrm{n}$

• $\rm Speed = distance / time$
  The time can be measured using data loggers or mobile phones. The speed of a sound along a metal rod or through water can also be investigated using direct methods.
• Echoes can be used with the source and observer standing a distance d in front of a tall wall. The rate of clapping can be adjusted to synchronize with the sound with their echoes. The time interval(t) can be measured.
  $\rm Speed = 2d/t$

• Diffraction is the spreading of a wave as it goes through an opening or passes an obstacle.
• The amount a wave diffracts depends on the relative size of the wavelength compared to the size of the opening or obstacle.
  

  	The wavelength is very small compared to the opening. The wave goes through without significant spreading. There is limited diffraction. This is how light passes through a window. Light has a very small wavelength compared to the window.
  	The wavelength is similar to the opening. The wave spreads after passing through the opening. There is significant diffraction. This is how sound passes through an open window. Sound has wavelength - similar to the size of the window.

• This is an application of the principle of superposition, for two coherent sources having similar amplitudes.
• The two sources are coherent if:
  • they have the same frequency
  • there is a constant phase relationship between the two sources.
  
  

• In the red regions constructive interference occurs where the waves are in phase. There is a region of destructive interference between these areas of constructive interference.
• The double slit experiment results in a regular pattern of light and dark strips across the screen as represented below.
  
• Bright fringes occur at angles θ where the path difference corresponds to a whole number of wavelengths. The waves interfere constructively.
  
  $d \sin \theta=\mathrm{n} \lambda$
  For small angles of $\theta$ in radians $\sin \theta \approx \theta$ when $\mathrm{n}=1$
  $d \theta==\lambda$
  
  The distance between the central and first bright fringe $\rm =s$
  $\rm \theta=s / D=\lambda / \mathcal d$
  $\lambda=d \rm s / D$