All measurement has a limit of precision and accuracy, and this must be taken into account when evaluating experimental results.

  • Qualitative data includes all non-numerical information obtained from observations, not from measurement.
  • Quantitative data are obtained from measurements and are always associated with random errors/uncertainties determined by the apparatus and by human limitations such as reaction times. 

Uncertainty and error in measurement

  • Random errors are caused by:
    • the readability of the measuring instrument
    • the effects of changes in the surrounding such as temperature variations and air currents
    • insufficient data
    • the observer misinterpreting the reading.
  • Random errors make a measurement less precise, but not in any particular direction. They are expressed as an uncertainty range, such as $\rm 25.05 \pm 0.05°C$.
  • The uncertainty of an analogue scale is $\pm$ (half the smallest division).
  • The uncertainty of a digital scale is $\pm$ (the smallest scale division).
  • Systematic errors occur when there is an error in the experimental procedure:
    Measuring the volume of water from the top of the meniscus rather than the bottom, or overshooting the volume of a liquid delivered in a titration will lead to readings which are too high.
    Heat losses in an exothermic reaction will lead to smaller observed temperatures changes.
  • Experiments are repeatable if the same person duplicates the experiment with the same results.
  • Experiments are reproducible if several experimentalists duplicate the results.
  • The precision or reliability of an experiment is a measure of the random error. If the precision is high then the random error is small.
  • The accuracy of a result is a measure of how close the result is to some accepted or literature value If an experiment is accurate then the systematic error is very small.
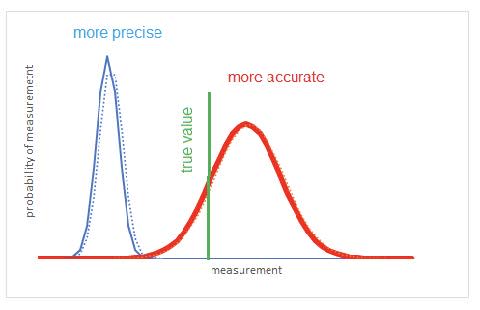
  • Random uncertainties can be reduced by repeating readings; systematic errors cannot be reduced by repeating measurements.
  • Precise measurements have small random errors and are reproducible in repeated trials. Accurate measurements have small systematic errors and give a result close to the accepted value.
  • The number of significant figures in any answer should reflect the number of significant figures in the given data.
  • When data is multiplied or divided the answer should be quoted to the same number of significant figures as the least precise.
  • When data is added or subtracted the answer should be quoted to the same number of decimal places as the least precise value.
  • When adding or subtracting measurements the total absolute uncertainty is the sum of the absolute uncertainties
  • When multiplying or dividing measurements the total percentage uncertainty is the sum of the individual percentage uncertainties. The absolute uncertainty can then be calculated from the percentage uncertainty.
  • If one uncertainty is much larger than others, the approximate uncertainty in the calculated result can be taken as due to that quantity alone.
  • The experimental error in a result is the difference between the recorded value and the generally accepted or literature value.
  • Percentage uncertainty = (absolute uncertainty /measured value) $\times 100\%$.
  • Percentage error = ((accepted value – experimental value)/ accepted value) $\times 100\%$.