Thermal energy transfer

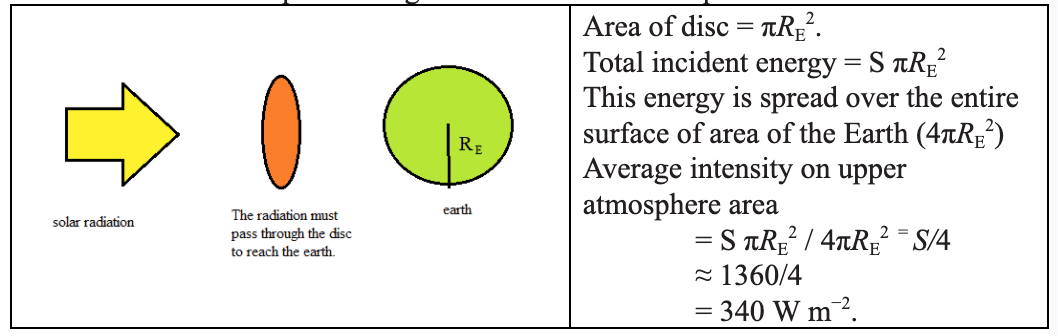
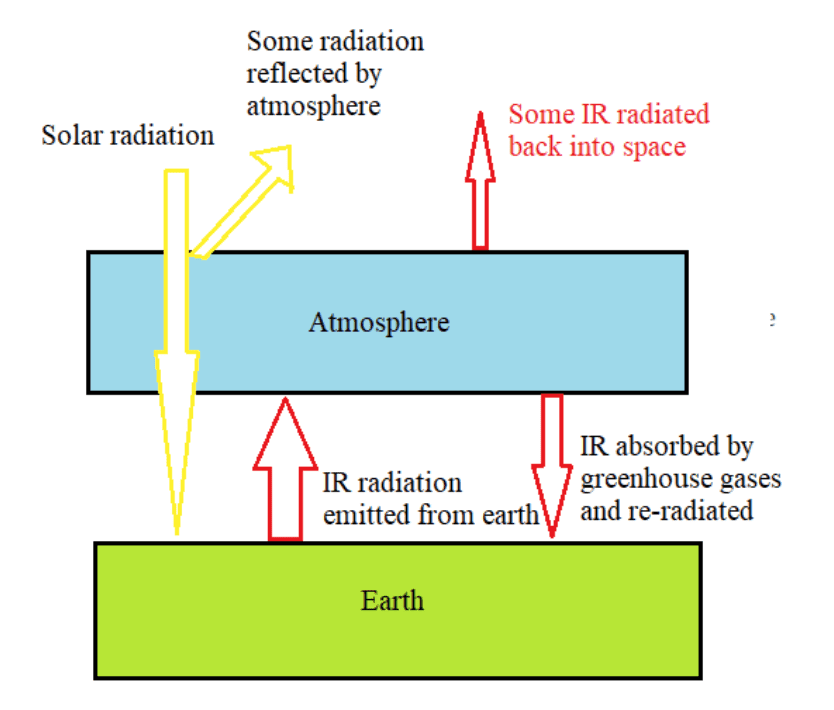
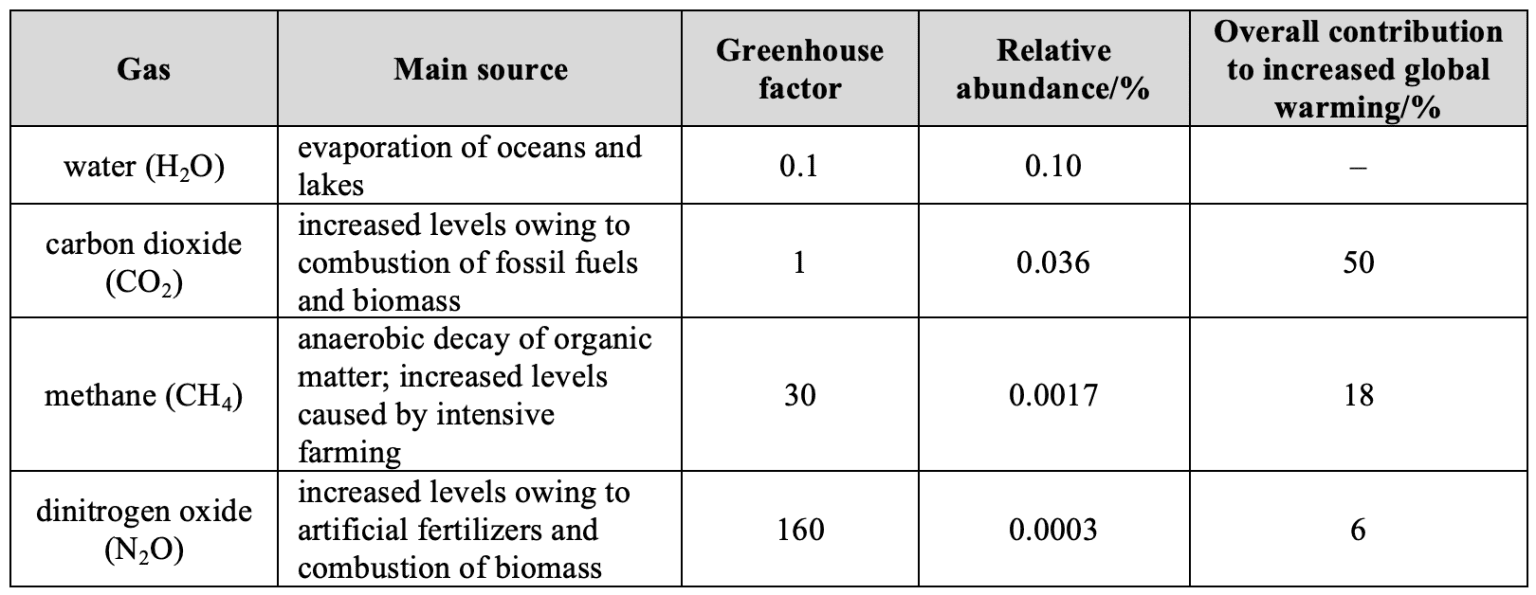
The energy transfer of the earth can be modelled by treating the earth as a black-body radiator and the atmosphere treated as a grey-body.

• Thermal Energy can be transferred by three distinct methods: conduction, convection and radiation.
• Energy can be conducted through solids by lattice vibrations, and the motion of free electrons.
• The rate of flow of energy $(\Delta \mathrm Q/\Delta t)$ through a solid depends on the temperature difference $\rm(\Delta T)$, the length $(l)$ of the piece of solid, the cross-sectional area $\rm (A)$ of the piece of solid and the material.
  $\Delta \mathrm Q/\Delta t = k \mathrm A \Delta \mathrm T/l$.
  $k$ is the thermal conductivity of the material.
• Gases (and many liquids) have low thermal conductivity. Thermal energy can instead be transferred by convection currents due to the movement of gas and liquid particles. Areas at a higher temperature have a lower density than areas at a lower temperature and molecules from these areas move upward carrying thermal energy.
• Convection cannot take place in a solid as the particles have a fixed position.
• Matter is not involved in the transfer of thermal energy by radiation.
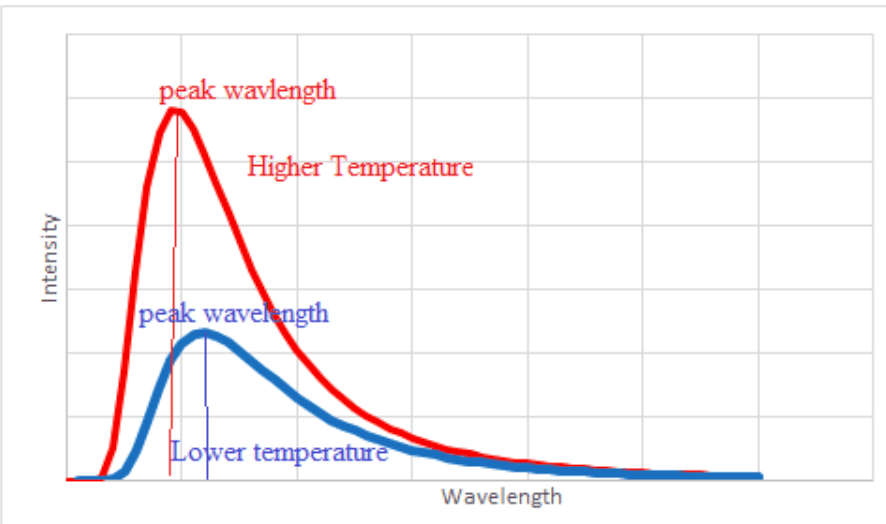
• All bodies emit energy in the form of electro-magnetic radiation. The rate of emission of energy depends on the temperature of the body and the nature of its surface. Most objects emit in the infra-red region of the electromagnetic spectrum.
• Similarly, all bodies absorb electro-magnetic radiation. The rate of absorption depends on the nature of the surface only.
• Dark coloured or dull surfaces both emit and absorb radiation better than light coloured or shiny surfaces.
• Radiation is the only method by which thermal energy van be transferred through a vacuum.

• A black body is an ideal object that absorbs all incident energy.
  The graph shows how the intensity of the radiation emitted from a black body changes as the temperature is varied. The electromagnetic radiation energy radiated by a body is distributed over an infinite range of wavelengths.
  
• The area under each curve represents the total power/area from the same surface irrespective of wavelength. It increases with absolute temperature.
• According to Stefan–Boltzmann law the power $\rm (P)$ emitted per unit area $\rm (A)$ of a black body : $\rm P / A=\sigma T^{4}$ where $\rm \sigma=5.67 \times 10^{-8} W ~m ^{-2} ~K ^{-4}$
• Most of the energy is radiated around a specific wavelength known as the peak wavelength $\rm (\lambda_{peak})$.
  According to Wien’s displacement law the peak wavelength $\rm (\lambda_{peak})$ is inversely proportional to the absolute temperature $\rm T$:
  $\rm \lambda_{\text {peak }}=2.90 \times 10^{-3} / T$
• Other surfaces can be considered as approximate black bodies with the emissivity, $\varepsilon$, acting as a correction factor: $\rm P=\varepsilon \sigma A T^{4}$
  $\rm \varepsilon=\scriptstyle\frac{\text{power radiated by object per unit area ar temp }T}{\text{power radiated per unit area by black body at temperature T}}$
  A black has an emissivity of $1$. Other bodies have values between $0$ and $1$.
  

  Surface	Emissivity
  black body ocean water ice dry land forests	$1.0$ $0.80-0.90$ $0.60-0.80$ $0.70-0.80$ $0.85-0.95$

• The intensity is the power received per unit area:
  $\rm I = P/A$
  If the source emits radially in all directions:
  $\rm I =P / 4 \pi d^{2}$ (where $d$ is the distance from the source).
• Some of the radiation received by a planet is reflected back into space. The fraction that is reflected is called the albedo, $\alpha$.
  $\mathbf{Albedo}~ \alpha=\dfrac{\text { reflected power }}{\text { total incident power }}$
  The albedo is different for different parts of the Earth depending on type of soil, depth of water, type of forestation and cloud cover. The Earth’s albedo varies daily and is dependent on season (cloud formations) and latitude.
  For example the albedo for snow is high $(0.85)$ since it reflects most of the radiation incident on it, whereas a dark forest has a low albedo $(\approx 0.10)$. The average for the planet Earth including its atmosphere is $30\%$.
• As discussed earlier the solar constant is $\rm S = 1~360~W~m^{-2}$. This is the energy received per square metre on a surface perpendicular to the Sun’s rays. To reach the earth solar radiation has to pass through a disc with a radius equal to that of the earth.
  
• As approximately $30 \%$ is reflected, the Earth's surface receives an average radiation intensity of $\rm 340 \times 0.70 \approx 255 ~W~ m ^{-2}$

Thermal equilibrium is reached when the power absorbed = power radiated.

Worked Example: The earth as a black body 
Calculate the temperature of the earth assuming it is a black body and the surrounding space has a temperature of $\rm 0~K$.

Solution
The incoming solar radiation reaching the surface has intensity $\rm I _{ av } =1360 / 4$
The Earth radiates power from all its surface. The power radiated $\rm I_{out} = P_{out} / A =\sigma T^{4}$
Equating the incident and outgoing intensities we get:
$\rm 1~360 / 4=\sigma T^{4}$
$\rm T^{4}=1~360 / 4 \sigma$
$\rm T =278~K$
This is not realistic as some radiation is scattered by the atmosphere.

Worked Example: The earth with an as a black body with an average albedo of $\bf0.30$
Calculate the temperature of the earth assuming it is a black body with an average albedo of $0.30$ and the surrounding space has a temperature of $\rm 0 K$.

Solution
The incoming solar radiation reaching the surface has intensity $\rm I _{ av }=(1-\alpha) S / 4=(1-\alpha) 1~360 / 4$
The Earth radiates power from all its surface. The power radiated $\rm P_{out}$
$\rm P_{out} / A =\sigma T^{4}$
Equating the incident and outgoing intensities we get:
$\rm (1-\alpha) 1~360 / 4=\sigma T^{4}$
$\rm T^{4}=(1-\alpha) 1~360 / 4 \sigma$
$\rm T =256~K$
This is $\rm 32~K$ lower than the Earth's average temperature of $\rm 288~K$. This model neglects the effect of the atmosphere temperature.

Worked Example: The earth with an emissivity of $\bf 0.60$ and an average albedo of $\bf 0.30$.
Calculate the temperature of the earth assuming it has an emissivity of $0.60$ and an average albedo of $0.30$.

Solution
Equating the incident and outgoing intensities we get:
$\rm (1-\alpha) 1~360 / 4=\varepsilon \sigma T^{4}$
$\rm T^{4}=(1-\alpha) 1~360 / 4 \sigma \varepsilon$
$\rm T =289~K$

• Ultraviolet rays are absorbed by ozone $\rm O_3$ in the upper atmosphere - the ozone layer.
• Visible light and other solar radiation are transmitted and absorbed by the earth’s surface.
• Longer-wave infra-red radiation is then re-emitted. This is absorbed by the greenhouse gases in the atmosphere, in contrast to the original visual light. The gases then re-radiate the energy in all directions including back to Earth.

• The greenhouse effect is a result of greenhouse gases in the atmosphere.
• Molecules exist in discrete energy states just like atoms. Infra-red radiation excites molecules and makes them vibrate more as they are excited to a higher energy state.
• Different molecules absorb radiation at different specific frequencies. The frequency of the radiation needs to match the frequency of the vibrations to be absorbed: an example of resonance.
• The molecules emit infra-red radiation in all directions when the molecule returns to a lower energy state.
  

• The use of fossil fuels increases the concentration of carbon dioxide in the atmosphere so more infra-red radiation is absorbed leading to an increase in the surface temperature.
• Deforestation has also reduced the amount of carbon dioxide absorbed during photosynthesis.
• The rising levels of methane are linked to increased levels of intensive farming.
• Similarly, the levels of nitrogen oxides are increasing because of the use of nitrogen-based fertilisers.

• There are some concerns that we may reach a tipping point when the levels of global warming cannot be reversed due to some positive feedback processes.  
• Global warming reduces ice/snow cover and the albedo. This increases the overall rate of heat absorption.
• Temperature increases reduces the solubility of $\rm CO_2$ in the sea and thus releases more greenhouse gases into the atmosphere.
• Temperature rises increase evaporation of water and the ability of the atmosphere’s ability to carry water vapour.