In the previous chapter we discussed how to find a function, given the derivative of the function. We will continue to build upon that in this chapter. Oftentimes we are interested in the area under a curve. Since it is a curve, it can be difficult to determine the area since there are no corners or 90 degree angles such as in a rectangle or triangle. However, we will first approximate the area under a curve by summing the areas of trapezoids, since the formula of a trapezoid is $\mathrm A=\dfrac{h}{2}(b_1+b_2)$ where $h$ is the height and $b_1$ and $B_2$ are the lengths of the parallel bases.

Example 1: Approximate the area under the curve of $f(x)=x^2+1$ and above the $x-$axis for $0\leq x \leq 2$ by calculating the areas of $2$ successive trapezoids.

Explanation: Sketching a graph of this yields the following picture:

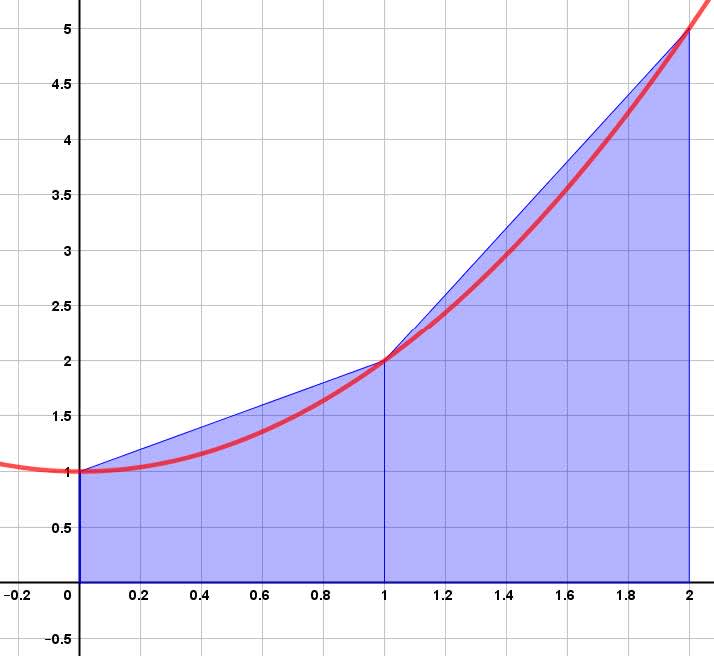
We will calculate the areas of $2$ trapezoids. Notice the height of each trapezoid is $1$ and the lengths of each base of each trapezoid is the value of the function at that particular $x$ value. Thus the total sum of these two trapezoids is:

$\mathrm{Sum}=\dfrac{1}{2}(f(0)+f(1))+\dfrac{1}{2}(f(1)+f(2))$
$\mathrm{Sum}=\dfrac{1}{2}(1+2)+\dfrac{1}{2}(2+5)$
$\mathrm{Sum}=\dfrac{3}{2}+\dfrac{7}{2}$
$\mathrm{Sum}=5$

It should be noted that this is an “over-estimate” and the true value of the area under the curve is less than $5$.

Recall: Given a polynomial of the form: $f′(x)=ax^n$ then an antiderivative of $f(x)$, is:

$f(x)=\dfrac{a}{n+1}x^{n+1}$

Without going into a formal proof, the total change in a system can be represented as the area between the curve and the x-axis between $x=a$ and $x=b$. This is referred to as a definite integral. It is calculated by finding the anti-derivative of a function and evaluating it between two $x$ values. Mathematically speaking,

$\displaystyle \int^b_a f(x)\mathrm dx=\mathrm F(b)-\mathrm F(a)$ where $a < b$ and $\mathrm F(x)$ is the antiderivative of $f(x)$.

Example 2: Evaluate $\displaystyle \int^2_0(x^2+x)\mathrm dx$

Explanation: Since the antiderivative of $x^2+x=\dfrac{x^3}{3}+\dfrac{x^2}{2}$, then:

$\displaystyle \int^2_0(x^2+x)\mathrm dx=\dfrac{x^3}{3}+\dfrac{x^2}{2} \overset{|^2}{|_0}$
$\displaystyle \int^2_0(x^2+x)\mathrm dx=\dfrac{2^3}{3} + \dfrac{2^2}{2} - \left(\dfrac{0^3}{3} + \dfrac{0^2}{2}\right)$
$\displaystyle \int^2_0(x^2+x)\mathrm dx=\dfrac{8}{3}+2−(0+0)$
$\displaystyle \int^2_0(x^2+x)\mathrm dx=\dfrac{14}{3}$
$\displaystyle \int^2_0(x^2+x)\mathrm dx=4.67$

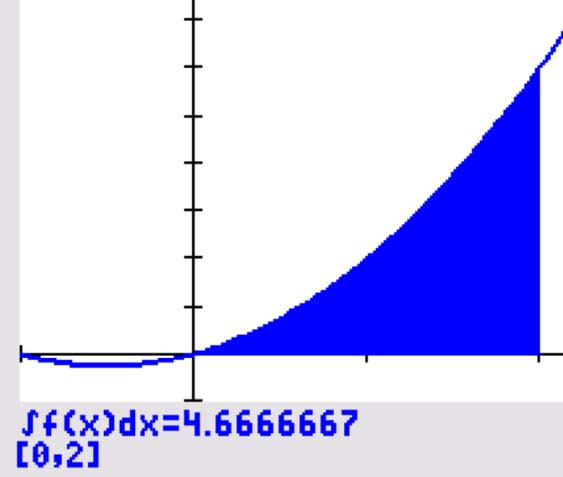
This can be seen in the following graph as the area under the curve of $x^2+x$ and above the $x-$axis between $x=0$ and $x=2$ using the 2nd TRACE command and option $7$ on the TI-84 CE graphing calculator.