The interaction of matter with radiation

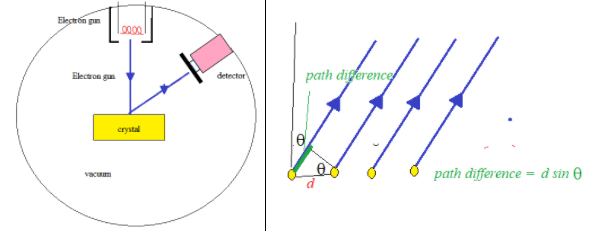
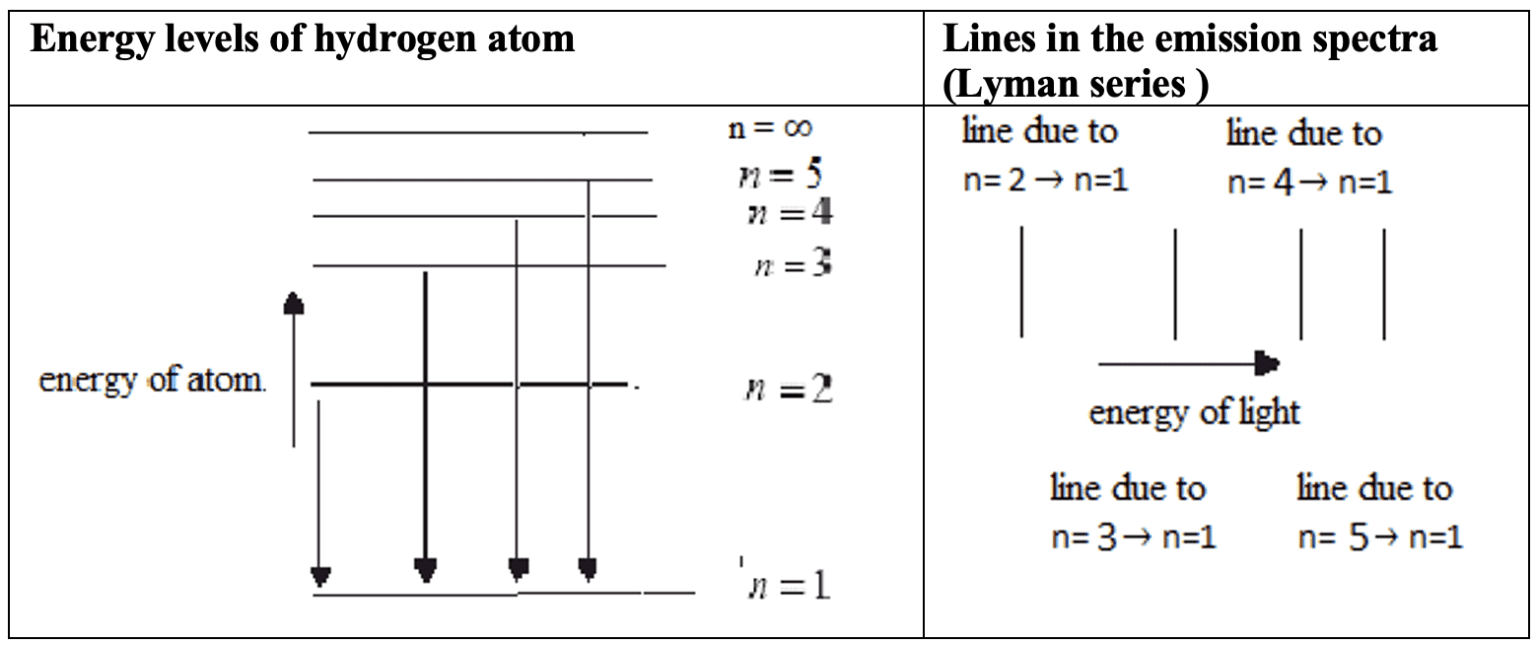
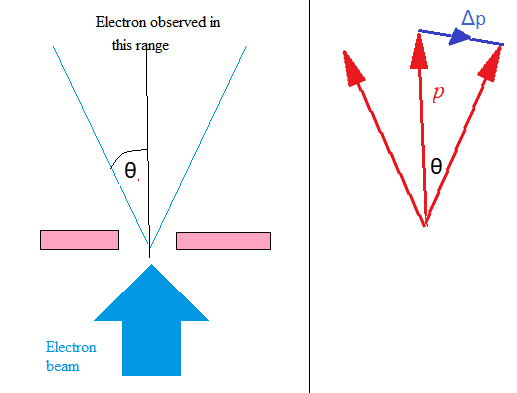
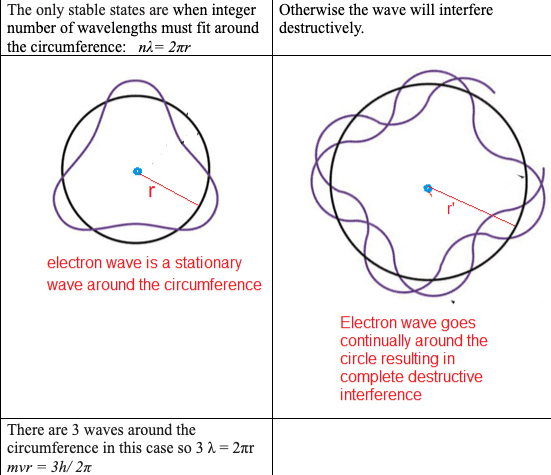
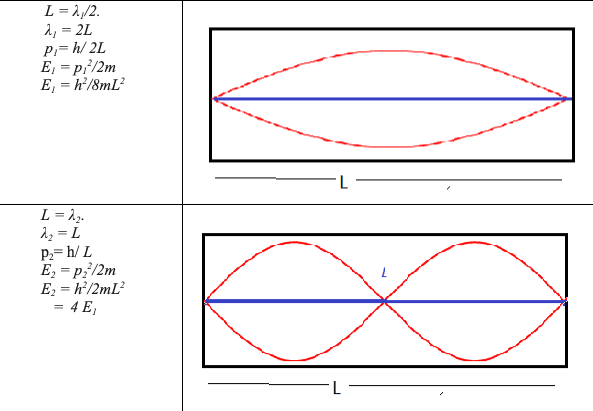
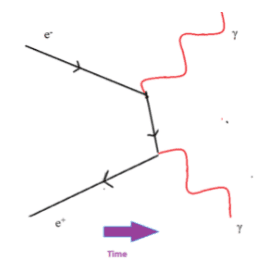
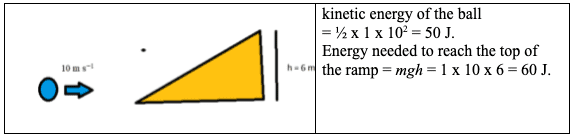
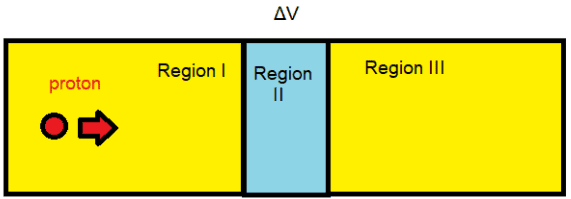
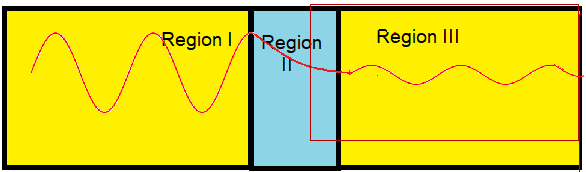
The microscopic quantum world behaves in a way that cannot be understood in terms of the macroscopic world of the ideas of the classical world based on our everyday experience. New ideas and concepts are needed. 

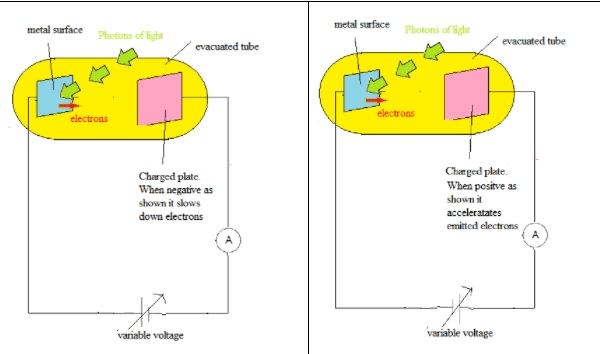
• Electrons are emitted from a metal surface when electromagnetic radiation is incident on the surface. 
• The kinetic energy of the emitted electrons $(\mathrm E_k)$ depends on the frequency of light. In classical theory the energy of the incident light waves depends on the intensity of light not the frequency.
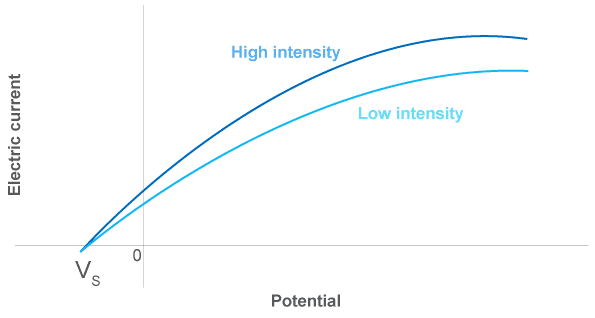
• The light intensity only affects the number of electrons emitted (i.e. the photocurrent).
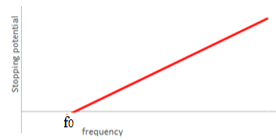
• There is a threshold frequency $\bf (\boldsymbol{f}_0)$ below which no electrons are emitted. In classical theory electrons would be emitted at all frequencies if the intensity was sufficiently high.
  
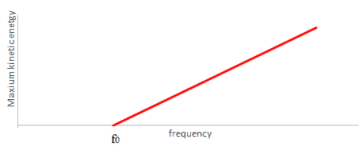
  From Einstein' explanation below:
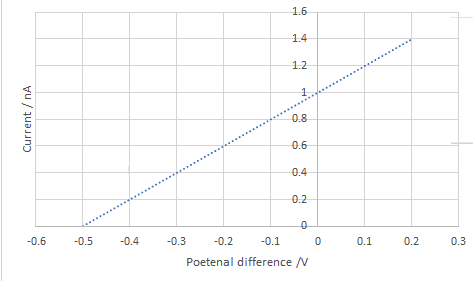
  $\mathrm E_{k}=h f-\varphi$
  $\mathrm E_{k} = hf - hf_0$
  $h$ can be determined from the gradient.
  The work function $(\varphi)$ can be determined from the horizontal intercept $f_{0}$.
  $\varphi = h f_0$
  $\mathrm E_k = hf - hf_0$
• Electrons are emitted with essentially no time delay. In classical theory it would take time for the electrons to collect the necessary threshold energy from the incident waves to escape.
• These facts are in contradiction with the classical wave theory of radiation and canonly be understood if light is considered to be a stream of particles called photons.

• Light is made up of particles of energy called photons. An electron is emitted from a metal surface when it absorbs one photon with sufficient energy for it to escape. The energy of each photon $\rm (E_{photon})$ is related to the frequency: $\mathrm{E_{photon}}= h f$ where $h$ is Planck's constant $\rm =6.63 \times 10^{-34}~J~s$
• If an electron absorbs a photon, we have $\rm E_{\text {photon}}=E_{\text {electron}}$
  The minimum energy to escape from the metal is called the work function $(\varphi)$. The extra energy from the photon is available as kinetic energy $(\mathrm E_{k})$ of the emitted electron.
  $\mathrm E_{\text {photon}}=h f=\mathrm E_{\text {electron }}=\varphi + \mathrm E_k$
  The work function is related to the threshold frequency $(f_{0})$:
  $\varphi = h f_{0}$
  $\mathrm E_{k}=h f-h f_{0}$
• As shown in the graph above
  • $\rm h$ can be determined from the gradient.
  • The work function can be determined from the horizontal intercept $f_{0}$
• The kinetic energy of the emitted electrons can be determined from the stopping potential $\bf(V_s)$. The emitted electrons can be accelerated or slowed by the charged plate. When the plate is negative it can slow down the electrons sufficiently that they don't reach it. The stopping potential $\bf(V_s)$ corresponds to a photocurrent of zero and the maximum kinetic energy of the emitted electrons.
  
  At the stopping potential: $\mathrm E_{k}^{\max }=\mathrm{e} \mathrm {V_s}$
  $h f=\varphi+\mathrm{e} \mathrm{V_s}$
  $\mathrm{V_s}=(h / \mathrm e) f+\varphi / \mathrm{e}$
  A graph of $f$ against the $\rm V_{s}$ gives a straight line with a positive gradient $(h / \rm e)$ with an intercept of $f_{0}$ on the horizontal axis. $h f_{0}$ corresponds to the work function $\varphi$.
  
  If the frequency of light is above threshold energy the current increases as the voltage increases from the stopping potential until a maximum is reached. This maximum current is limited by the number of electrons that escape from the metal target which is in turn limited by the intensity of the photons striking the metal target.
  
• Increasing the intensity of the UV light increases the number of photons and the number of emitted electrons.   
• The work function can be obtained from the stopping potential and the wavelength of light as shown in the worked example.

Worked Example

Light of a wavelength of $\rm 456~nm$ is incident on a metal plate. The current varies with potential difference as shown.

Determine the work function of the metal.

Solution

Note the use of $h c=1.24 \times 10^{-6} \rm ~eV~m$, makes calculations much faster. This constant is in the IB data booklet.
From the graph $\rm V_s=0.50~V$
$\mathrm{e V_s} = h f - \Phi$ we deduce that:
$\Phi=h c / \lambda- \rm e V_{s}$
$\Phi=(1.24 \times 10^{-6} / 4.96 \times 10^{-7})-0.50$
$\rm \Phi=2.20~eV$

• The latter section shows that light which was classically considered as a wave could be understood as a stream of particles called photons.  
• Historically we asked the question: is light a particle or a wave? Now we say its behaviour can only be explained with reference to a wave and particle model.
• This wave-particle duality is expressed by the de Broglie’s hypothesis which states that all moving particles with a momentum $(p)$ show wave behaviour with a wavelength $(\lambda)$ given by $\lambda = h/p$
  $h$ is the Planck constant.
  This relationship can be understood from Einstein’s energy relationship and Plank’s relationship for a photon, but it applies to all moving particles:
  $\mathrm E=m c^{2}=h f$
  Equating $m c$ with the "momentum $(p)$ " of a photon: $p c=h f$
• Note the conventional formula for momentum, $p = mv$, does not strictly apply to photons and other particles with zero mass. The momentum $(p)$ of the photon is $p = \mathrm E/c$ but the de Broglie’s does apply to all particles including photons.

• The wave nature of electrons is observed in electron diffraction.  In the Davisson and Germer electron diffraction experiment. A beam of fast electrons is directed at a crystal. The electrons diffract off the regularly spaced crystal atoms and create a diffraction pattern, similar to that produced by light.
  
• The electrons are scattered by the top layer of atoms. When the path difference between successive scattered electron waves is
  • an integer multiple of the wavelength, there is constructive interference,
  • a half integer number of wavelengths there is destructive interference.   
• The diffraction pattern observed can only be explained if the electrons have wavelength properties.
• The image produced is very similar to that of diffraction of ordinary light by a circular aperture and calculations of the wave from the observed diffraction pattern agrees with the de Broglie formula.

• In the Bohr model for the hydrogen atom the electron circulates around the nucleus of one proton in circular orbits. The evidence from atomic line spectra suggests that only certain orbitals were allowed. Bohr suggested that these orbits had fixed multiples of angular momentum $(\mathrm L = mvr)$. The orbits were quantized in terms of angular momentum.
  $\mathrm L=n h / 2 \pi$
  
• The energy of the electron can be calculated from this model.

From Topic 10

Electrostatic force provides the centripetal force:

Equation 1:
$m v^{2} / r=\mathrm e^{2} / 4 \pi \varepsilon_{\rm o} r^{2}$
$v^{2}=\mathrm e^{2} / 4 \pi \varepsilon_{\rm o} m r$

Equation 2:
$\mathrm E_{p}=\mathrm Q q / 4 \pi \varepsilon_{\rm o} r=-\mathrm e^{2} / 4 \pi \varepsilon_{\mathrm o} r$
$\mathrm E_{k}=+\mathrm e^{2} / 8 \pi \varepsilon_{\mathrm o} r$
$\mathrm{E_T} =-\mathrm e^{2} / 8 \pi \varepsilon_{\mathrm o} r$

From the Bohr model

$n h / 2 \pi=m v r$
$r=n h / 2 \pi m v$
$r^{2}=n^{2} h^{2} / 4 \pi^{2} m^{2} v^{2}$

Substituting for $v^{2}$ (from Equation 1)
Equation 3:
$r^{2}=\left(n^{2} h^{2} / 4 \pi^{2} m^{2}\right) \times 4 \pi \varepsilon_{o} m r / \mathrm e^{2}$
$r=\left(n^{2} h^{2} \varepsilon_{\mathrm o} / \pi m \mathrm e^{2}\right)$

Combing Equation 2 and Equation 3: $\mathrm{E_T}=-\mathrm e^{2} / 8 \pi \varepsilon_{\mathrm o} \times\left(\pi m e^{2} / n^{2} h^{2} \varepsilon_{o}\right)$ $\mathrm{E_T} =-m e^{4} / 8 h^{2} \varepsilon_{o}{^2}\left(1 / n^{2}\right)$

The energy levels can only have certain values based on n: they are quantised.
This equation can be expressed in following form: $\mathrm E_{n}=-13.6 / n^{2} \mathrm{eV}$.

• The emission spectrum of atomic hydrogen consists of lines of particular wavelengths. In 1885 a Swiss schoolteacher called Johann Jakob Balmer found that the visible wavelengths followed a mathematical equation.
  $1 / \lambda=\mathrm{R}_{\mathrm{H}}\left(1 / 2^{2}-1 / m^{2}\right)$ with $m>2$ and $\mathrm{R}_{\mathrm{H}}$ is a constant
  Other series exist which follow the more general equation:
  $1 / \lambda=\mathrm{R}_{\mathrm{H}}\left(1 / n^{2}-1 / m^{2}\right) m$ and $n$ are integers with $m > n$ and $\mathrm{R}_{\mathrm{H}}$ is a constant.
  $n=1$ corresponds to series of line in the ultraviolet region of the spectrum.
  $n=3$ corresponds to series of line in the infrared region of the spectrum.
  

• If an electron falls from one energy level, $\mathrm{n}_{\text {initial }}$ to a lower level, $\mathrm{n}_{\text {final }}$, then a photon of light is emitted. The energy of the photo $\rm(E_{\text {photon }})=$ the energy change in the atom $\rm \Delta E_{\text {atom }}$.
  $\mathrm E_{\text {photon}}=\Delta \mathrm E_{\text {atom}}$ $=-m e^{4} / 8~h^2 \varepsilon_{\rm o}{^{2}}(1 / n_{\text {initial}}^{2})$ $-$ $m \mathrm e^{4} / 8 h\mathrm e 0^{2} r(1 / n_{\text {final }}^{2})$
  $hf = me^{4} / 8 ~h\varepsilon_{\rm o}{^{2}}\left(1 / n_{\text {final }}{^{2}}-1 / n_{\text {initial }}{^{2}}\right)$
• For the Lyman series $n_{\text {final }}=1$
  So the lines will become close together as $n_{\text {initial }}$ increases.
• This theoretical result can be compared to the empirical Rydberg equation.
  And the value of the empirical constant $\mathrm{R}_{\mathrm{H}}$ seems to be a product of fundamental constants.
  $1 / \lambda=me^{4} / 8 ch^3 \varepsilon_o{^2}(1 / n_{\text {final}}{^2}-1 / n_{\text {initial }}{^2}$
  $1 / \lambda=\mathrm{R_H}\left(1 / n^{2}-1 / m^{2}\right)$
  $m>n$

• The Bohr model has the following strengths: 
• • It predicts the Rydberg formula and is in excellent agreement with experimental measurement.
  • The Rydberg constant can be calculated from other (known) constants and the agreement with experimental data is excellent.
• The limitations to this model are:
  • the same approach cannot be used to predict the emission spectra of other atoms or ions with more than one electron.
  • the Bohr postulate about angular momentum has no theoretical justification in classical physics, which predicts that an electron should not be stable in circular orbits around a nucleus. Accelerated electrons should radiate energy and so spiral into the nucleus.
  • it does not explain the relative intensity of the different lines.

• Another fundamental problem with the Bohr model is that it assumes the electron’s trajectory can be precisely described. This is now known to be impossible, as any attempt to measure an electron’s position will disturb its motion. The act of focusing radiation to locate the electron gives the electron a random ‘kick’ which sends it hurtling off in a random direction.
• Particles sometimes behave like waves and waves sometimes behave like particles, so that we cannot clearly divide physical objects as either particles or waves.
• Consider a beam of electrons moving towards a circular aperture. The width of the beam of width is $b$ so it can pass through the aperture. The uncertainty in the horizontal position $\Delta x \approx b/2$
• Considering now the electrons as a wave we can predict that diffraction will occur.
  
  
• From Topic 9 the angle by which the electron is diffracted is given by: $\Theta \approx \lambda / b$
  The uncertainty of the momentum ranges over the same angle: $\Theta=\Delta p / p$
  $\Theta=\lambda / b \approx \Delta p / p$
  But $b \approx 2 \Delta x$ so: $\lambda / 2 \Delta x \approx \Delta p / p$
  $\Delta x \Delta p \approx \lambda p / 2$
  The de Broglie wavelength of an electron $(\lambda)=h / p$ and $\lambda p=h$
  $\Delta x \Delta p \approx h / 2$
  This simple treatment is only approximate. A more correct result is $\Delta x \Delta p=h / 4 \pi$
• This is one expression of Heisenberg’s Uncertainty Principle which shows that we cannot know where an electron is at any given moment in time – the best we can hope for is a probability picture of where the electron is likely to be. The possible positions of an electron are spread out in space in the same way as a wave is spread across a water surface.

• As we have seen, all the electrons can be considered to have wave properties. Bohr’s postulate can be explained using a wave model of the electron. To be stable the electron must form a stationary wave around the circumference of a hydrogen atom.
  
  We obtain Bohr's relationship from de Broglie hypothesis.
  $n h / p=2 \pi r$
  $n h / 2 \pi=m v r$
• The allowed orbits in the Bohr model of hydrogen are those for which an integral number of electron wavelengths fit on the circumference of the orbit: they are standing waves. Standing waves do not transfer energy this partially which explains why the electrons do not radiate when in the allowed orbits.

• As we have seen the electron can be considered to have wave properties and its position and momentum cannot be known with certainty. Only a probability description of its location is possible at a given time. These ideas are encapsulated in the Schrödinger model of the electron. 
• Erwin Schrödinger (1887–1961) provided a quantum model for the behaviour of electrons in all atoms – not just hydrogen.
• The Schrödinger theory assumes as a basic principle that there is a wave associated with the electron. This wavefunction, ψ(x, t), is a function of position $x$ and time $t$.
• The probability $mathrm P(x, t)$ that an electron will be found within a small volume $\rm \Delta V$ near position $x$ at time $t$ is: $\mathrm P(x, t)=|\psi(x, t)|^{2} \Delta \rm V$
• The theory only gives probabilities for finding an electron somewhere – it does not pinpoint an electron at a particular point in space. This is a radical departure from classical physics, where objects have well-defined positions.
• Schrödinger’s theory gives all the results that Bohr derived but it also predicts the probability that a particular transition will occur. This is necessary in order to understand why some spectral lines are brighter than others. The Schrödinger theory explains the atomic spectra for all elements.
• According to the Schrödinger theory, electrons do not follow well defined orbits but instead move in a region of space called an atomic orbital.  An atomic orbital is a region around an atomic nucleus in which there is a $90\%$ probability of finding the electron. The shape of the orbitals will depend on the energy of the electron. When an electron is in an orbital of higher energy it will have a higher probability of being found further from the nucleus.

• Consider an electron confined in a region of size $\rm L$.
  
• The electron can only move back and forth along a straight line of length $\rm L$.
• Then the uncertainty in position must satisfy $\Delta x \approx \rm L / 2$ and so the uncertainty in momentum must be $\Delta p \approx h / 4 \pi \Delta x$ $\approx h / 2 \pi \rm L$
• The kinetic energy $\mathrm E_{\mathrm{K}}=p^{2} / 2 m \approx \Delta p^{2} / 2 m$ $=h^{2} / 8 \pi^{2} \rm m L^{2}$
• We may apply this result to an electron in the hydrogen atom. The size of the region within which the electron is confined is about $\rm L \approx 10^{-10}~m$.
  $\rm E_{K} \approx h^{2} / 8 \pi^{2} ~m L^{2}$
  $\approx\scriptstyle\left(6.63~ \times~ 10^{-34}\right)^{2}~ /~ 8 \pi^{2}(9.1~ \times~ 10^{-31})(10^{-10})^{2}$
  $\approx 6 \times 10^{-19} \mathrm{~J} \approx 4 \mathrm{eV}$
  This is an approximate value for the electron's kinetic energy.
• The uncertainty principle explains why an electron cannot exist within a nucleus of an atom. The above calculation can be repeated imagining an electron being trapped inside the nucleus of size $10^{-14} \mathrm{~m}$.
  $\rm E_K \approx h^2 / 8 \pi^2~mL^{2}$
  $\approx\scriptstyle \left(6.63 ~\times 10^{-34}\right)^{2}~ / ~8 \pi^{2}\left(9.1~ \times~ 10^{-31}\right)\left(10^{-14}\right)^{2}$ $=10^{8} \times 4 \mathrm{eV}$
  An electron with this energy would have enough energy to escape the atom.
• This shows that the uncertainty principle allows us to make approximate estimates for various quantities.

• Another method for obtaining approximate energies is the electron box method.
• As the electrons has no probability of being out of the box only a set of stationary waves are possible:
  
• More generally $\mathrm E_{n}=n^{2} h^{2} / 2 ~\rm m L^{2}$
  Notice that imposing boundary conditions (e.g. nodes at the ends) determines the wavelength which in turn determines the energy.
  Using the uncertainty principle $\mathrm E_{\mathrm{K}} \approx h^{2} / 8 \pi^{2} ~\rm m L^{2}$ and using the stationary wave method $\mathrm E_{\mathrm{K}} \approx h^{2} / 8 ~\rm m L^{2}$ Both methods are approximate only and do not necessarily give the same answers.

• Consider an electron of kinetic energy $\rm E_K$ that collides with a positron (the anti-particle of the electron) that moves in the opposite direction with the same kinetic energy.
  
• As shown in the Feynman diagram the particle and antiparticle annihilate each other and produce two photons.
  
• Total energy of the electron-positron $\mathrm{(E_T)} = 2(m c^{2} + \rm E_K)$.
• As the momentum before collisions $=0$ two photons are produced which travel in opposite directions with the same energy and wavelength.
  $2 \mathrm E_{\text {photons }}=2(m c^{2} + \rm E_{K})$.
  $\mathrm E_{\text {photons }}=(m c^{2}+\rm E_{K})$.
  $h f=(m c^{2}+\rm E_K)$
  $h c / \lambda=m c^{2}+\rm E_K$
  $\lambda=h c /\left(m c^{2}+\rm E_K\right)$
• The longest wavelength will be emitted when the particles are more or less at rest, $\rm E_K=0$, and so in this case:
  $\lambda_{\max} =h c / m c^{2}$
  $=h / m c=2.4 \times 10^{-12} \mathrm{~m}$
• The reverse process is also possible – photons of sufficient energy can produce a pair of matter and antimatter particles. Their energy goes into the rest masses of the particles with any excess going into the kinetic energy. 
• A single photon cannot materialise into a particle – anti-particle pair because such a process would not conserve energy and momentum. Instead, a single photon can make use of a nearby nucleus to produce a particle – anti-particle pair. The nucleus is not changed in the interaction but it ‘absorbs’ some of the momentum allowing the interaction to occur.
• This process of pair creation, in effect, is a case where energy is converted into matter.

• Consider the scattering of a photon by an electron
  The uncertainty of location of the electron is related to the wavelength of the light:
  $\Delta x=k \lambda$
  The time for a photon to travel this distance $\Delta t$
  $\Delta x=c \Delta t=k \lambda \\
  c \Delta t / k=\lambda$
  The photon has an energy $\mathrm E_{\text {photon }}=h f$
  The photon could change the energy of the electron by this amount $E$ so the uncertainty to the energy of the electron.
  $\Delta \rm E_{\text {electran }}=E_{\text {photon }}$ $=h f=h c / \lambda$
  $\lambda=h c / \Delta \rm E_{\text {electron }}$
  Equating the two expressions for $\lambda$
  $h c / \Delta \rm E_{\text {electron }}$ $=c \Delta t / k$
  $h / \Delta \mathrm E_{\text {electron }}=\Delta t / k$
  $h k =\Delta \mathrm E \Delta t$
  $\Delta t$ is the time period when the energy uncertainty is $\Delta \rm E$
  This shows that the uncertainty principle also applies to measurements of energy and time. This is a general relationship and a more precise treatment gives $k=1 / 4 \pi$ : $\Delta \mathrm E \Delta t \geq h / 4 \pi$
• If the uncertainty of the energy of a state is $\Delta\rm E$, then the lifetime of the state $\Delta t$ such that: $\Delta \mathrm E \Delta t \geq h / 4 \pi$

• In the situation below the ball would not be expected to reach the top of the ramp as it does not have sufficient kinetic energy.
  
• The ramp acts as a 'potential barrier' to the ball.
• Similarly consider a proton of total energy $\rm E$ entering a region of positive electric potential $\Delta \mathrm{V}$. The proton needs sufficient energy to cross the potential barrier.
  Energy needed $\rm =e \Delta V$.
  
• If the total energy of the proton is less than $\rm e \Delta V$ the proton has zero probability of moving from region $\rm A$, through region $\rm B$ and into the 'forbidden' region $\rm C$.
• Given that there is some uncertainty about the energy of the proton the situation is less clear in the quantum world and tunnelling is possible. A particle can escape it if it "borrows' an amount of energy $\Delta \mathrm{E}$ provided it 'pays it back' in a time $\Delta \mathrm{t}$ such that the uncertainty principle applies. $\Delta \mathrm E_{\text {borrow }} \approx h / 4 \pi \Delta t$
• The longer the barrier, the more time it takes the particle to tunnel and the smaller the energy the particle can "borrow".
• The wavefunction of the protons in each of the three regions $\rm I, II$ and $\rm III$ must be smooth with no jumps and no corners: it can 'leak' into region $\rm III$.
  
• In region $\rm II$ the wave function is decreasing but at the beginning of region III it isn’t zero and there is some probability that the proton is in region $\rm III$ although it is forbidden in classical energy terms. 
• The proton has tunnelled through the potential barrier.
• Three factors affect the probability of transmission:
  • the smaller the mass $m$ of particle the greater the quantum effects and greater the chance of tunnelling
  • the smaller the width w of the barrier the shorter the time interval $\Delta t$ and the greater the energy available $\rm\Delta E$.
  • the difference $\Delta \rm E$ between the energy of the barrier and that of the particles.
• The transmission probability for electrons is greater than for protons, as they have a smaller mass.
• Note the de Broglie wavelength in region $\rm III$ is the same as in region $\rm I$. The particles that emerge in region $\rm III$ have the same momentum and energy as they did in region $\rm I$ as they have returned the borrowed energy available from the uncertainty principle.
• Tunnelling has very many practical applications, including the scanning tunnelling microscope: a microscope that can give pictures of atoms. It also offers a mechanism by which an alpha particle can leave an atomic nucleus despite the strong nuclear forces they experience within the nucleus.