In the previous chapter, the derivative evaluated at a point, or instantaneous rate of change at a moment in time, is the slope of the tangent line. Since a line travels through infinitely many points, all we need is one point that the line travels through and along with the slope, we can determine the equation of the tangent line. Which point should we choose? The most obvious answer is the point that the line is tangent to at the function. To see this, consider the polynomial function $f(x)$ below:

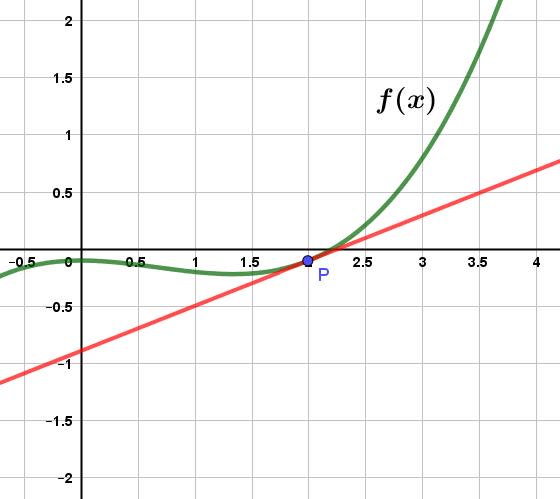
To determine the equation of this tangent line we would need to determine the slope evaluated at point $\rm P$. This can be determined using the Power Rule. Once this is found, then all we need to do is insert the $(x,y)$ coordinate of the point $\rm P$ into the equation of a line. Point-Slope form of a line would be useful in this case.

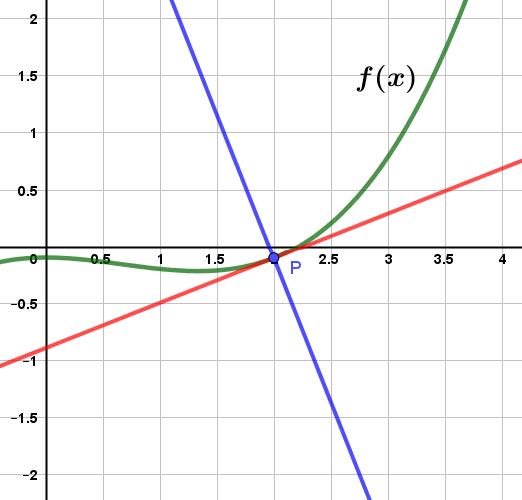
Another topic assessed in the A&A SL curriculum is the equation of the perpendicular line to the tangent line at the point $\rm P$. This is referred to as the normal line.

Remember: The normal line to a function at a point $P$ is the line that is perpendicular to the tangent line at the same point $P$.

Recall that perpendicular lines have slopes that are negative reciprocals of each other. Since the normal line travels through the same point, all we need to do is to take the slope of the tangent line, multiply it by negative one and reciprocate it. A graph of this is shown below with a red tangent line and a blue normal line at the point $\rm P$.

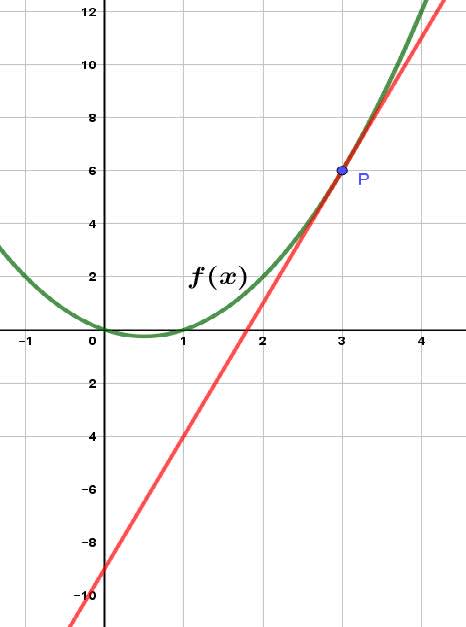
Example: Determine the equation of the tangent line to $f(x)=x^2−x$ at the point $\rm P(3,6)$.

$f′(x)=2x−1$
$\Rightarrow f′(3)=2(3)−1=5$

Therefore, the slope of the tangent line is $5$.

Using point-slope form of a line $y−y_1=m(x−x^1)$ produces the equation of the tangent line $y−6=5(x−3)$. Sometimes it is useful to change this into slope-intercept form of line which is $y=5x−9$.

This can be seen in the graph below. Note the $y-$intercept is $−9$.