Standing waves

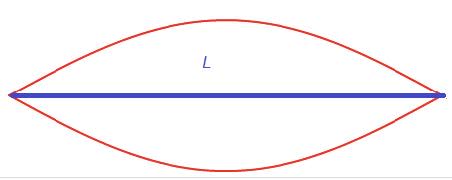
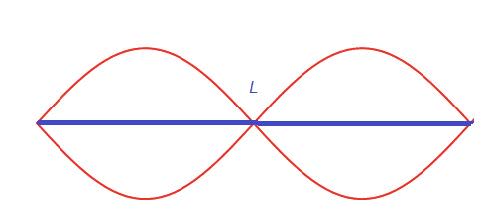
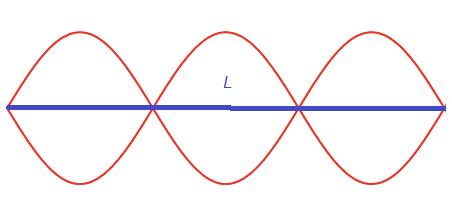
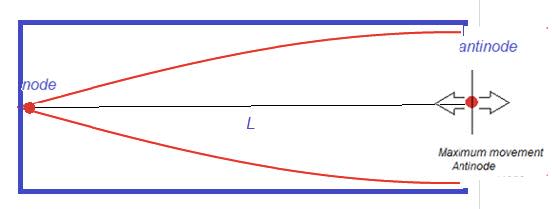
• A standing wave is formed when two identical travelling waves moving in opposite directions meet and superpose.
• The superposition of the two travelling waves is called a standing wave as the wave pattern does not move to the right or left. Only the amplitude changes.
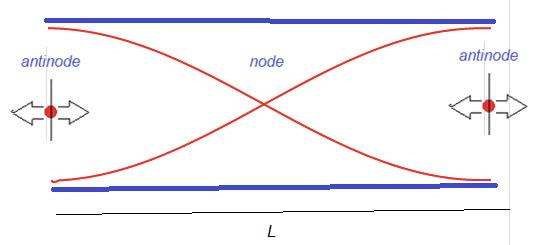
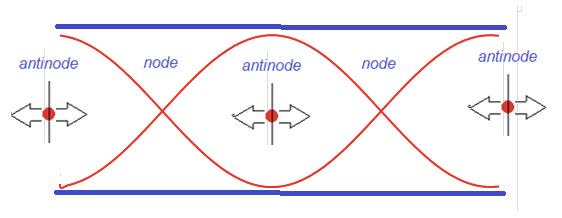
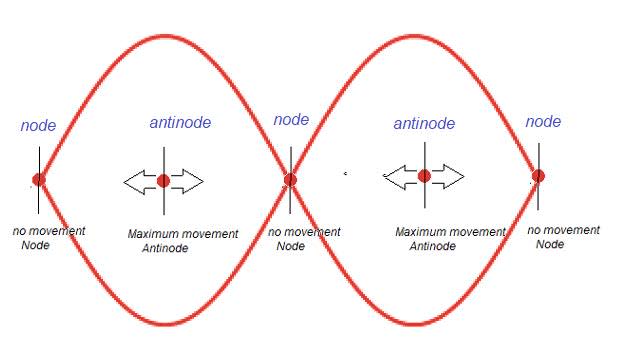
• The points which always have zero displacement are called nodes.
• The points which always have a maximum displacement are called antinodes.
• The distance between two consecutive nodes is half a wavelength.

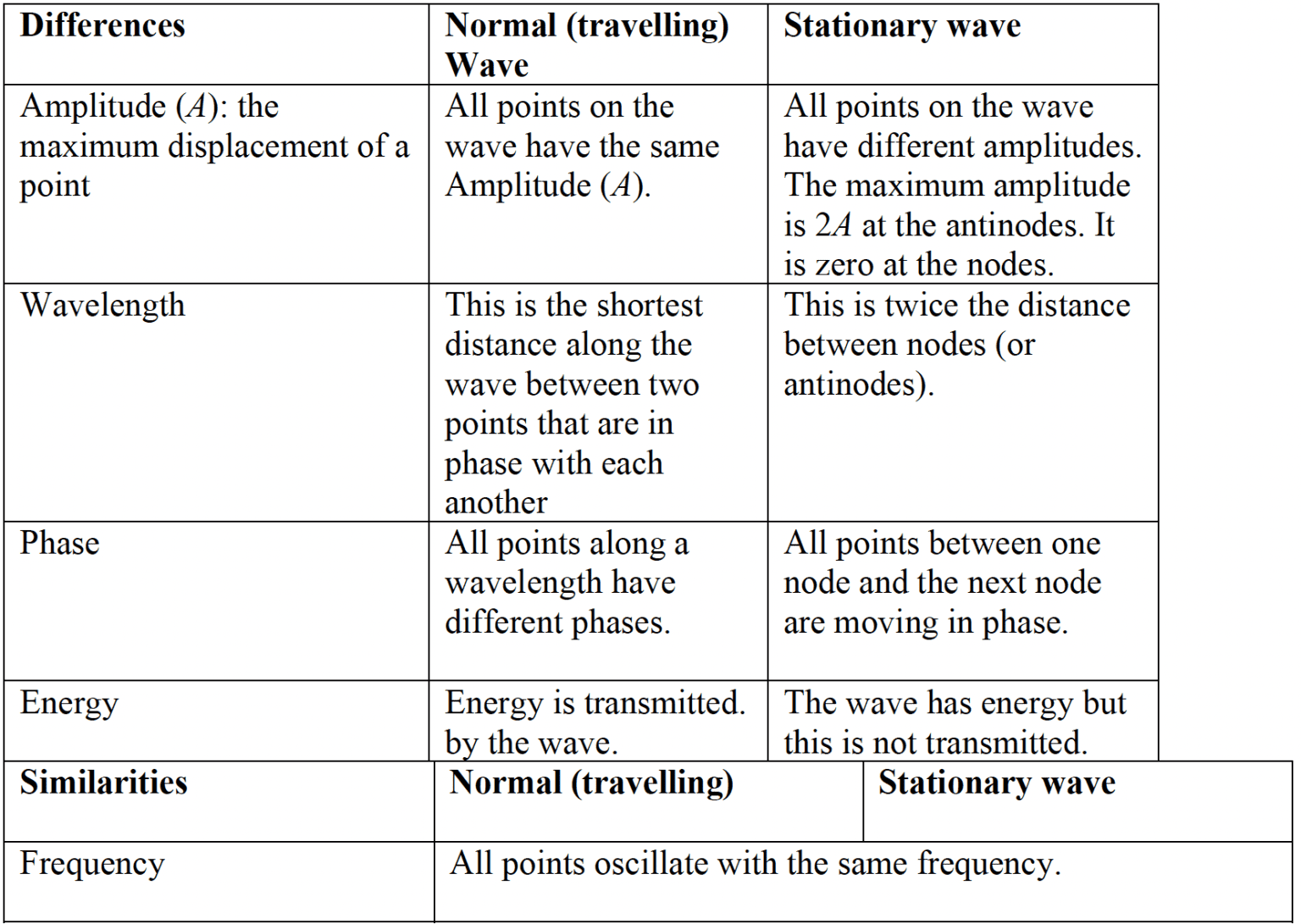
A comparison with a normal travelling wave and a standing wave

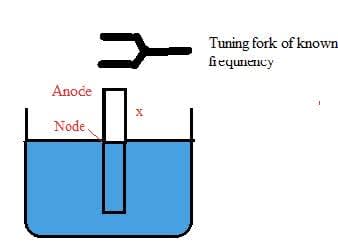
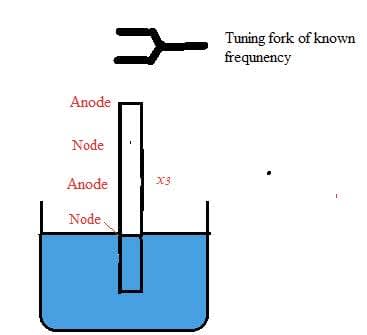
• Standing wave can be created using sound or light waves.
• As sound is a longitudinal wave the antinodes are the points which have the maximum displacement parallel to the direction of the initial travelling waves.
  
• Musical instruments involve the creation of a standing sound wave inside the instrument.

The boundary conditions of the system specify the conditions that must be met at the edges (the boundaries) of the system when standing waves are taking place.

• The waves on a string are transverse.
• The ends on a string cannot move as they are nodes. Let the length be $\rm L$.
  

  First harmonic (fundamental) The length $\rm L$ corresponds to $\lambda/2$. $\lambda / 2 =\mathrm{L}$ $\lambda_{1}=2 \mathrm{~L}$ $f_{1}=v / \lambda_{1}$ $f_{1}=v / 2 \rm L$
  Second harmonic The length corresponds to $\lambda$. $\lambda_{2} =\mathrm{L}$ $f_{2} =v / \lambda_{2}$ $f_{2} =v / \mathrm{L}$ $f_2=2 f_{1}$
  Third harmonic The length corresponds to $3/2 \lambda_3$ $3 / 2 \lambda_{3}=\mathrm{L}$ $\lambda_{3}=2 / 3 \mathrm{~L}$ $f_{3}=v / \lambda_{3}$ $f_{3}=3 v / 2 \mathrm{~L}$ $f_3=3 f_{1}$

• The sound waves in a pipe are longitudinal.
• There is a node at the closed end as the molecules cannot move and an antinode at the open end.
• Note a harmonic is named by the ratio of its frequency to that of the first harmonic.
  The first and third harmonics are shown. There is no second harmonic.
  

  First harmonic (fundamental) The length $\rm L$ corresponds to $\lambda_1/4$. $\lambda_{1} / 4 .=\mathrm{L}$ $\lambda_{1}=4 \mathrm{~L}$ $f_{1}=v / \lambda_{1}$ $f_{1}=v / 4 \rm L$
  Third harmonic The length $\mathrm{L}=$ $3 \lambda_{3} / 4$ $\lambda_{3}=4 \mathrm{~L} / 3$ $f_{3}=3 v / 4 \mathrm{~L}$ $f_3=3 f_{1}$

• Only odd harmonics are present in a pipe open at one end.

• There is an antinode at both ends as the molecules can move freely.
  

  First harmonic $\mathrm L=\lambda_{1} / 2$ $\lambda_{1}=2 \mathrm{~L}$ $f_{1}=v / \lambda_{1}$ $f_1=v / 2~\rm L$
  Second harmonic $\mathrm{L} = \lambda_{2}$ $f_{2} =v / \lambda_{2}$ $f-2 = v / \mathrm{L}$ $f_2 = 2 f_{1}$

• The speed of sound can be measured using a resonance tube.
  A tuning fork of known frequency $(f)$ is struck, and the distance $x$ is measured. $v=f \lambda$.
  

  	$x_{1}=\lambda / 4$ $\lambda=4 x_{1}$ $v=4 f x_{1}$
  	$x_{3}=3 \lambda / 4$ $\lambda=4 x_{3} / 3$ $v=4 f x_{3} / 3$