Single-slit diffraction

📝 Mini-cours GRATUIT

Single-slit diffraction

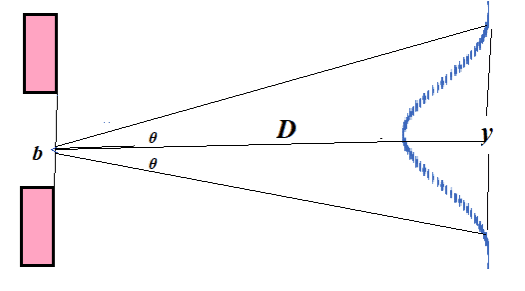
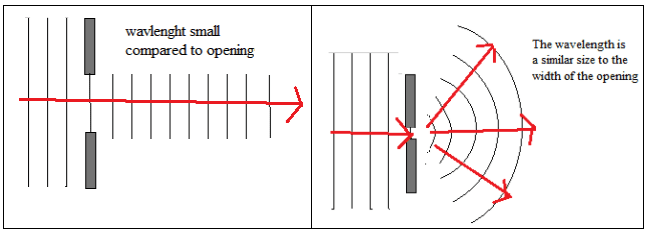
Diffraction is the spreading of a wave as it goes through an opening or passes an obstacle. Diffraction is a property that characterises wave behaviour.

Consider waves of wavelength $\lambda$ from the top and the middle of the rectangular slit. moving towards the right with a slit of width $b$. The path difference is $½~b\sin \theta$.

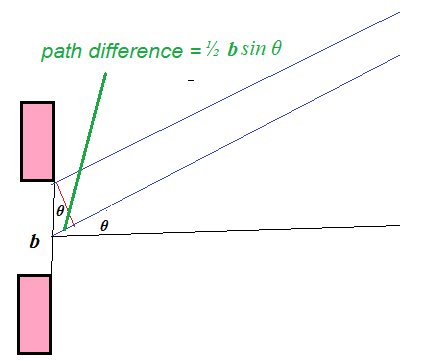
As the angle is very small (in radians), this path difference is approximately $½~b~\theta$
If this path difference is half a wavelength there is destructive interference and there is a minimum at a diffraction angle $\theta: \theta=\lambda$
$½~b~\theta = ½~\lambda$
$b~\theta=\lambda$
Considering other waves below the top and just below the middle of the slit can apply the same conditions to deduce the same general result: $\theta=\lambda / b$
When $\theta=0$ the waves arrive in phase and there is constructive interference
The intensity of the wave varies as a function of the angle $\theta$ as shown in the graph.
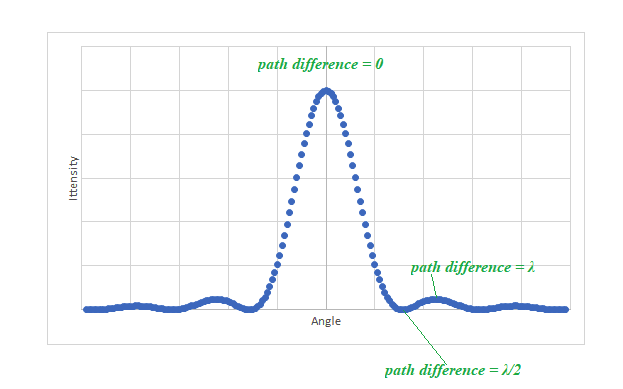
There is non-zero intensity even when $\theta \neq 0$, as the wave diffracts.
Maxima occur when there is constructive interference with a path difference of $n \lambda$
Minima occur when there is destructive interference with a path difference of $(2 n+1) / 2 ~\lambda$

The reasoning for a circular aperture of diameter is more complex but the angle follows a similar equation: $\theta = 1.22 ~\lambda/b$
The angle of the first minima for:
- Rectangular aperture
- $\theta=\lambda / b$
  $b$ is the width of the slit.
- Circular aperture
- $\theta \approx 1.22 ~\lambda/ b$
  $\mathrm{b}$ is the diameter of the aperture.
Let the distance between the aperture and the screen be $\rm D$. Let the width of the central maximum of a single aperture diffraction pattern be $y$.