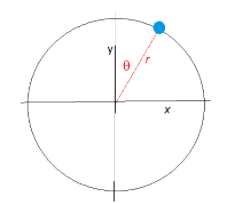
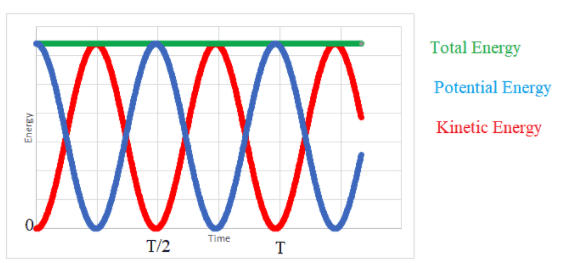
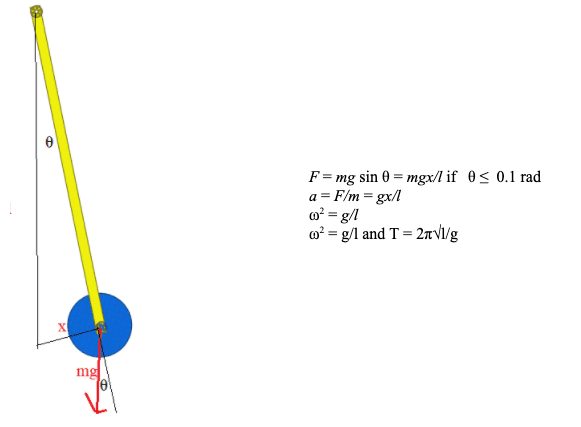Simple harmonic motion (SHM)

Simple harmonic motion involves an exchange between kinetic and potential energy in a system.

• In SHM the acceleration (or the net force) is proportional to the displacement from equilibrium but in the opposite direction.
  $a=-\omega^{2} x$ where $\omega$ is a constant called the angular frequency.
• This can be expressed as $\mathrm{d}^{2} x / \mathrm{d} t^{2}=-\omega^{2} x$
  And has the solutions:
  

  (a) $x=x_{0} \sin \omega t$ $\mathrm{d} x$ $\mathrm dt=v$ $=+ x_{0} \omega \cos \omega t$ $\mathrm{d}^{2} x / \mathrm{d} t^{2}$ $=a$ $=-x_{o} \omega^{2} \sin \omega t$ $=-\omega^{2} x$

  (b) $x=x_{0} \cos \omega t$ $\mathrm{d} x / \mathrm{d}t=v$ $=-x_{0} \omega \sin \omega t$ $\mathrm{d}^{2} x / \mathrm{d} t^{2}$ $=a$ $=-x_{0} \omega^{2} \sin \omega t$ $=-\omega^{2} x$

  The format of the relationships, (a) or (b), depends on the displacement at time $(t)= 0$.
• The period for a complete cycle is $\mathrm{T}$. This corresponds to an angle $2 \pi$.
  $\omega=2 \pi / \mathrm{T}$
• Other relationships follow from these equations:
  $x^{2}=x_{0}{^{2}} \sin ^{2} \omega t$
  $v^{2}=\omega^{2} x_{0}{^{2}} \cos ^{2} \omega t \quad v^{2} / \omega^{2}=x_{0}{^{2}} \cos ^{2} \omega t$
  $x^{2}+v^{2} / \omega^{2}=x_{0}{^{2}} \sin ^{2} \omega t+x_{0}{^{2}} \cos^{2} \omega t$
  $x^{2}+v^{2} / \omega^{2}=x_{0}{^{2}}\left(\sin^{2} \omega t+x_{0}{^{2}} \cos^{2} \omega t\right)$
  $x^{2}+v^{2} / \omega^{2}=x_{0}{^{2}}$
  $v^{2} / \omega^{2}=x_{0}{^{2}}-x{^{2}}$
  $v^{2}=\omega^{2}\left(x_{0}{^{2}}-x^{2}\right)$
  $v=\sqrt{\omega^{2}}\left(x_{0}{^{2}}-x^{2}\right)$

• Consider an object moving in a circle of radius $r$ with an angular frequency of $\omega$.
  $x=r \sin \theta$
• The max value of $x=x_{0}=r$
  $x=x_{0} \sin \omega t$
• The horizontal and vertical components of circular motion follow the equation of SHM.
  $x=x_{0} \sin \omega t$
  $y=y_{0} \cos \omega t$
  

• During SHM, energy is interchanged between kinetic energy and potential energy. When there is no damping, the total energy remains constant.
  $\mathrm{E_{kinetic}}=½~m v^{2}=½~ m \omega^{2}$ $\left(x_{0}^{2}-x^{2}\right)$
  The kinetic energy is equal to the total energy when $x=0$
  $\rm E_{total}=½ ~m \omega^{2}$ $\left(x_{0}{^{2}}\right)$
• The total energy in SHM is proportional to:
  • the mass $\mathrm{m}$
  • the (amplitude)$^{2}$
  • the (angular frequency)$^{2}$
• The potential energy can be expressed as the difference between the total energy and the kinetic energy:
  $\rm E_{Potential} = E_{total} - E_{kinetic}$ $= ½~m \omega^{2} x^{2}$

The energy changes during simple harmonic motion:

Note the kinetic energy and potential energy undergo two cycles in the period $\rm T$.

Mass on a vertical spring

• Assuming:
  • the mass of the spring is negligible
  • no damping
  • the spring obeys Hooke’s law with spring constant, $k$
  • the gravitational field strength $g$ is constant

$\mathrm F=-k x \quad \mathrm F=m a$
$m a=-k x$
$a=-k / m x$ so $\omega^{2}=k / m$
As $\mathrm{T}=2\pi / \omega$
$\mathrm{T}=2 \pi \sqrt{ \dfrac{m}{k}}$

Note from before: $\rm E_{Potential}= E_{total} - E_{kinetic}$ $=½~\mathrm m \omega^{2} x^{2}$ $=½~\mathrm m(k / \mathrm{m}) x^{2}=½ ~k x^{2}$
As expected for elastic potential energy.

The simple pendulum with length $l$ and mass $m$

• Assuming that:
  • the mass of the string is negligible
    damping is negligible
  • the maximum angle of swing is small $\rm (\leq 0.1~rad)$
  • the gravitational field strength g is constant
  • the length of the pendulum is constant.
    

• Note the mass of the pendulum bob, m does not affect the time period of the pendulum, $\rm T$.