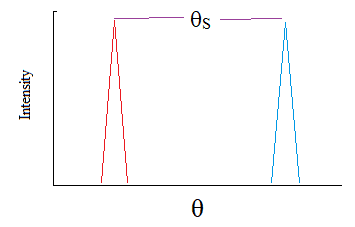
Resolution

Resolution places an absolute limit on the extent to which an optical or other system can separate images of objects.

• Resolution is the ability to distinguish two separate objects as separate objects.  
• Light from two point sources diffracts, when it passes through an aperture. If the two sources are separated by a small angle the diffraction patterns will merge and the two sources will appear as one.
  

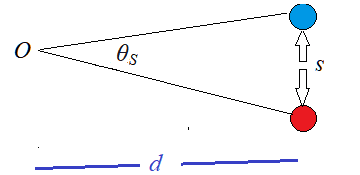
• The two objects in the diagram are at a distance $d$ from the observer $\rm (O)$ and separated by a distance $\rm s$. The angular separation is $\rm \theta_S \approx s / d$
  
• To examine whether two sources are resolved the angular separation $\theta_{\mathrm{S}}$ must be compared with the resolution angle, $\rm \theta_{R}$, between the central maximum and the first minimum in a diffraction pattern.
  

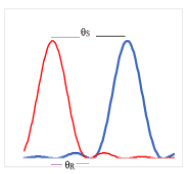
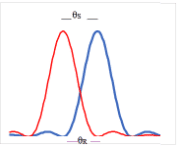
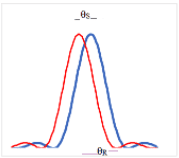
  $\rm  \theta_{S} > \theta_{R}$ The sources are clearly resolved.	$\rm \theta_{S} = \theta_{R}$ The sources are just resolved. The central maximum of one coincides with the first minimum of the other.	$\rm \theta_{S} < \theta_{R}$ The sources are not resolved

• The angle $\rm \theta_{R}$ between the maximum and minimum for a circular aperture $=1.22 \lambda / b$ Where $b$ is the diameter of the circular aperture used to collect light from the sources.
• According to the Rayleigh criterion: two sources are just resolved if the central maximum of the diffraction pattern of one source falls on the first minimum of the other: $\rm \theta_{S}=\theta_{R}=1.22 \lambda/ \mathrm{b}$

• An important characteristic of a diffraction grating is its ability to resolve, i.e. see as distinct, two lines in a spectrum that correspond to wavelengths $\lambda_{1}$ and $\lambda_{2}$ that are close together. 
• If the wavelengths are close to each other the angles at which the lines are observed will also be close to each other and so difficult to resolve.
  In the diagram if the angular separation of the two lines is too small the two lines will not be seen as distinct.
  

• The resolving power $\mathrm{R}$ of a diffraction grating is defined in terms of the wavelengths $\lambda_{1}$ and $\lambda_{2}$ that can just be resolved. $\lambda_{\text {avg }}$ is the average of $\lambda_{1}$ and $\lambda_{2}$ and $\Delta \lambda$. is their difference:
  $\rm R=\lambda_{avg} / \Delta \lambda$
  The higher the resolving power, the smaller the differences in wavelength $\Delta \lambda$ that can be resolved.
• The resolving power $\mathrm{R}$ is related to $\mathrm{N}$, the total number of slits on the diffraction grating: $\rm R=m N$ where $m$ is the order at which the lines are observed:
  $\rm R == mN = \lambda_{avg} / \Delta \lambda$
  $\rm \Delta \lambda=\lambda_{avg}mN$
  If the difference in wavelengths to be resolved is small a grating with a large number of rulings needs to be used.