Rate expressions can only be determined empirically and these limit possible reaction mechanisms.
The Rate expression
- The rate equation expresses the reaction rate as a function of reactant concentrations:
For a reaction with reactants $\rm A$ and $\rm B$:
$\mathrm{Rate} = k [\mathrm A]^m [\mathrm B]^n$- $\rm [A]$ and $\rm [B]$ are the concentrations of the reactants
- $m$ and $n$ are the orders of reaction with respect to $\rm A$ and $\rm B$ respectively
- $m + n =$ overall order of reaction
- $k$ the rate constant is affected by temperature, and the units of k are determined from the overall order of the reaction.
- The half-life of a chemical reaction is the time taken for the reactant concentration to decrease to half the initial concentration. The half-life is constant for a first order process.
- Rate equations can only be derived from empirical data. Concentration–time and rate–concentration graphs can be used to represent zero-, first-, and second-order reactions.
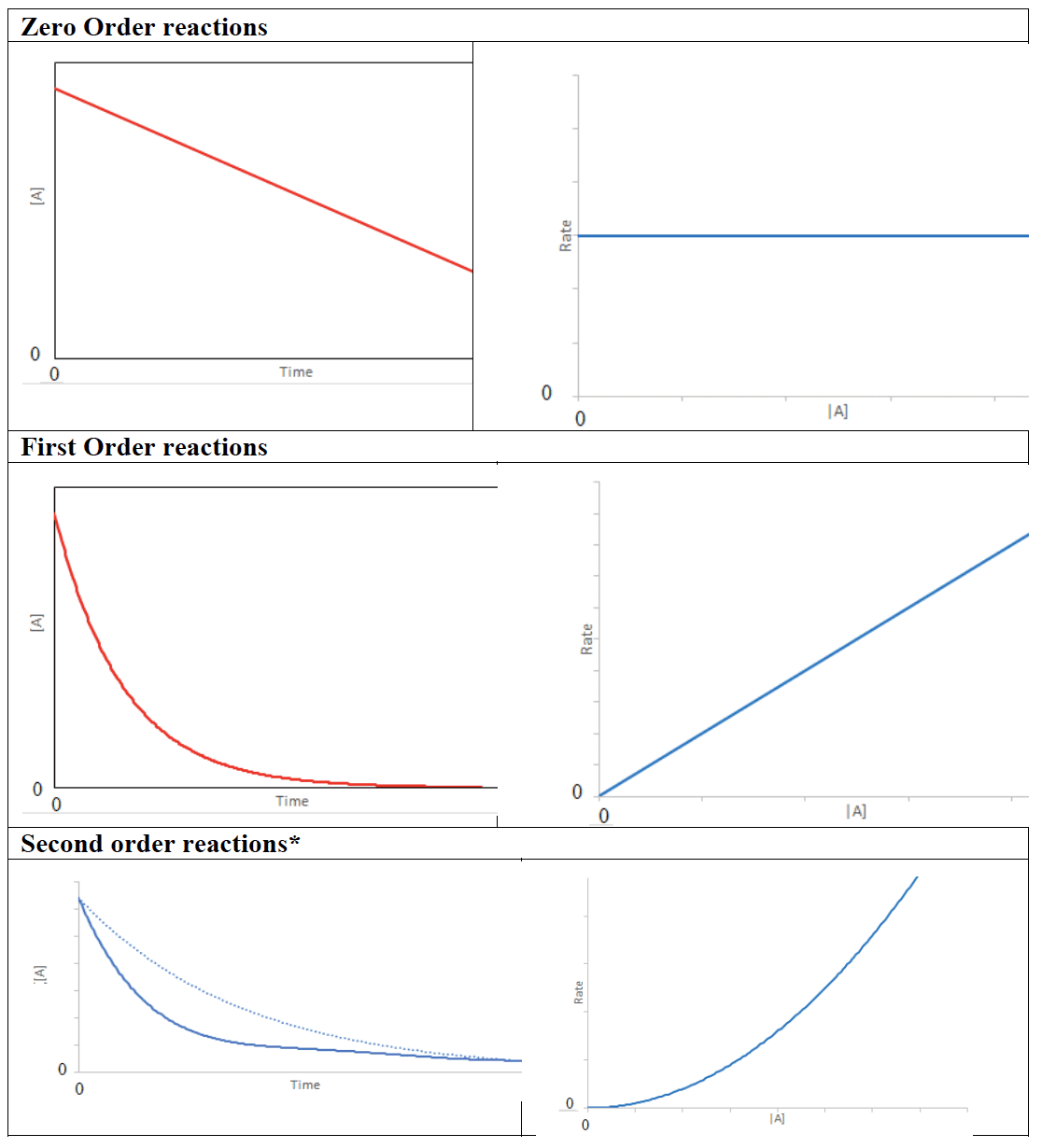
*The first order exponential curve is shown with a dotted line as reference.
Worked Example
The rate of the reaction between nitrogen(II) oxide and hydrogen was investigated :
$\rm 2NO(g) + 2H_2(g)$ $\rm \rightarrow N_2(g) + 2H_2O(g)$
The results are presented below:

- Deduce the reaction orders with respect to $\rm NO$ and $\rm H_2$.
Solution
$\mathrm{Rate} = k [\mathrm{NO}]^m [\mathrm H_2]^n$
Considering reaction $1$ and $2$.
$\require{cancel}\dfrac{\rm Rate_2}{\rm Rate_1} = \dfrac{\cancel{k} (0.0400)^m \cancel{(0.0060)^n}}{\cancel{k} (0.0100)^m \cancel{(0.0060)^n}} = \dfrac{0.6400}{0.0400}$
$\dfrac{(0.0400)^m}{(0.0100)^m} = 16$
$4^m = 16$
$m = 2$
The reaction is second order with respect to NO.
Considering reaction $1$ and $3$.
$\require{cancel}\dfrac{\rm Rate_3}{\rm Rate_1} = \dfrac{\cancel{k} (0.0200)^2 (0.0240)^{\cancel{n}}}{\cancel{k} (0.0100)^2 (0.0060)^{\cancel{n}}} = \dfrac{0.6400}{0.0400}$
$(2)^2 (4)^n = 16$
$4^n= 4$
$n = 1$
The reaction is the first order with respect to $\rm H_2$.
- Use the answers (1) to state the rate expression and the overall order of reaction.
Solution
$\mathrm{rate} = k\rm [NO]^2[H_2]$.
Overall reaction order: $2 + 1 = 3$.
- Calculate the value of the rate constant at the temperature of the investigation.
Using the data from experiment $1$.
Solution
$k (0.0400)^2 (0.0060) = 0.6400$ $= \dfrac{0.6400}{(0.0400)^2 (0.0060)} = 66~700$
For the units
$\rm mol~dm^{-3}~s^{-1} = (mol~dm^{-3})^3\mathcal k$
$\rm mol~dm^{-3}~s^{-1} = mol^3~dm^{-9}\mathcal k$
$k = \rm (mol^{-2}~dm^6)s^{-1}$
$k = \rm 66~700~dm^6~mol^{–2}~s^{–1}$
$k = \rm 6.7 \times 10^4~dm^6~mol^{-2}~s^{-1}$
Mechanisms
- Many reactions proceed in a series of small steps known as elementary steps.
- The molecularity is the number of reactant particles taking part in an elementary step.
- The rate of the reaction is determined by the slowest reaction step: the rate determining step (RDS) It is the step with the highest activation energy.
- A catalyst alters the reaction mechanism by introducing a new RDS with a lower activation energy
- An intermediate is a chemical species that is formed and consumed during the overall chemical reaction. Intermediates are neither reactants nor products and never appear in rate expressions.
- The order of the reaction is determined by the molecularity of the rate-determining step.
- A proposed mechanism for a reaction must be consistent with:
- the overall reaction’s stoichiometry.
- kinetic data derived from experiment.
Worked Example
The following mechanism is proposed for a reaction:
$\rm NO(g) + NO(g) \rightleftharpoons N_2O_2(g) \qquad fast$
$\rm N_2O_2(g) + H_2(g)$ $\rm \rightarrow N_2O(g) + H_2O(g) \qquad slow$
$\rm N_2O(g) + H_2(g)$ $\rm\rightarrow N_2(g) + H_2O(g) \qquad fast$
- Deduce the overall equation for the reaction.
Solution
Adding equations:
$\rm 2NO(g) + N_2O_2(g) + H_2(g) + N_2O(g)$ $+$ $\rm H_2(g)$ $\rm\rightarrow N_2O(g) + 2 H_2O(g) + N_2O_2(g) + N_2(g)$
Simplifying:
$\rm 2NO(g) + 2H_2(g) + N_2O(g)$ $\rm\rightarrow N_2O(g) + 2H_2O(g) + N_2(g)$
$\rm 2NO(g) + 2H_2(g)$ $\rm \rightarrow 2 H_2O(g) + N_2(g)$
- Deduce the rate expression.
Solution
The $\rm RDS$ is the slowest step:
$\mathrm{Rate} = k \rm [N_2O_2(g)] [ H_2(g)]$
$\rm N_2O_2$ is a not one of the reactants: it is an intermediate. We need to express it a reactant concentration:
Using the equilibrium law from Topic $7$.
$\rm K = \dfrac{[N_2O_2(g)]}{[NO(g)]^2}$
$\rm [N_2O_2(g)] = K [NO(g)]^2$
$\mathrm{Rate} = k \rm [NO(g)]^2 [H_2(g)]$
 Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
