Quadratic Functions

Have you ever thrown a ball into the air? Have you noticed that the harder you throw it, the longer the ball stays in the air? Yet, what comes up must come down. How long will the ball stay in the air? How far will it travel? What will be the maximum height the ball will reach? All of these questions can be answered by solving quadratic equations.

Every quadratic function can be written as $f(x)= ax^2 + bx +c$ where $a$, $b$, $c$ are real numbers with $a\neq 0$.

Every quadratic equation of the form $ax^2+bx+c=0$ can be solved using the quadratic formula which is: $x=−b\pm\sqrt{\dfrac{b^2−4ac}{2a}}$

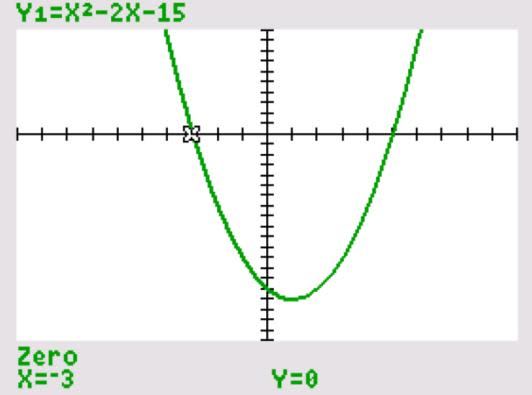
Example 1: Solve: $x^2−2x−15=0$. Here $a=1$, $b=−2$, $c=−15$.
Thus, $x= \dfrac{−(−2)\pm\sqrt{(−2)^2−4(1)(−15)}}{2(1)}$ $=\dfrac{2\pm \sqrt{4+60}}{2}$ $=\dfrac{2\pm\sqrt{64}}{2} = \dfrac{2\pm 8}{2}$

Notice there are always two solutions, namely:

$x=\dfrac{2+8}{2}=5$ and $x=\dfrac{2−8}{2}=−3$

This can also be seen using the TI-84 CE graphic display calculator using the 2nd Trace command zero:

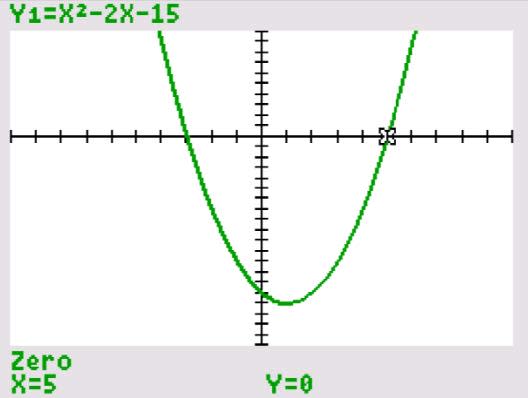It is important to understand that the “zeros” of the quadratic equation are in fact the $x$-intercepts for the quadratic function.

Example 2: Solve the quadratic equation: $2x^2−x−2=0$

Here $a=2$, $b=−1$, $c=−2$. Thus:

$x=\dfrac{−(−1)\pm\sqrt{(−1)^2−4(2)}}{(2)2}$ $=\dfrac{1\pm\sqrt{1+16}}{4}$ $= \dfrac{1\pm\sqrt{17}}{4}$

Again, there are two solutions, namely: $x=\dfrac{1+\sqrt{17}}{4}=1.28$ and $x=\dfrac{1−\sqrt{17}}{4}=−0.781$

The discriminant of the quadratic formula is $b^2−4ac$ and oftentimes is referred to as the most important part of the quadratic formula. This is because it determines the nature of the solutions: $2$ real solutions $(b^2−4ac>0)$ the square root of a positive number, $1$ real repeated solution $(b^2−4ac=0)$ the square root of $0$, or $2$ imaginary solutions $(b^2−4ac<0)$ the square root of a negative number.

Example 3: Determine the value of $a$ if $ax^2+2x−8=0$ has $2$ real solutions.

Evaluating the discriminant implies that $b^2−4ac>0$. Therefore:

$(2)^2−4a(−8)>0$
$4+32a>0$
$32a>−4a>−\dfrac{4}{32}$

$a>−18$ and remember $a\neq 0$

Thus $ax^2+2x−8=0$ will have $2$ real solutions provided $a>−\dfrac{1}{8}$ with $a\neq 0$.