Power generation and transmission

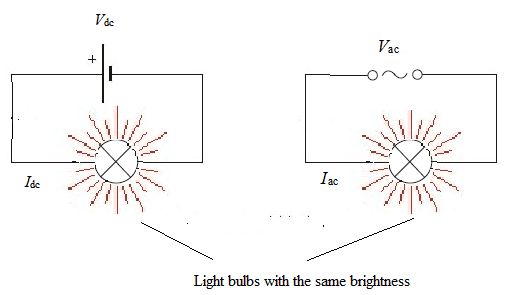
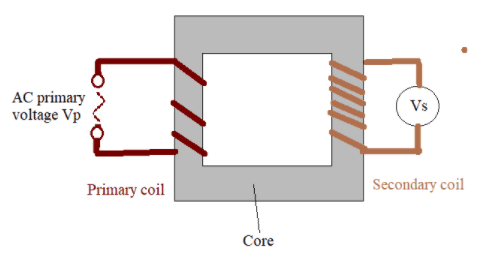
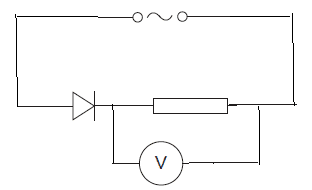
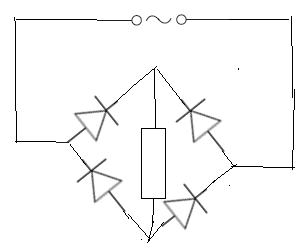
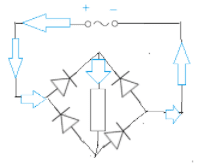
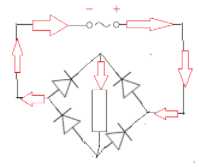
Alternating current $(ac)$ electricity is the most convenient to generate, transform and transmit.

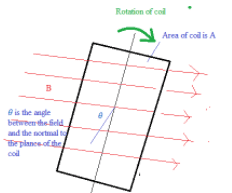
• Electricity for commercial and home use comes mainly from generators that involve a coil rotating in a magnetic field.
  $\Phi=\mathrm{BA} \cos \theta$
  If $\omega$ is angular frequency, $\theta=\omega t$
  $\Phi=\mathrm{BA} \cos \omega \mathrm{t}$
  $\varepsilon=-\Delta \Phi / \Delta \mathrm{t}=\omega \mathrm{BA} \sin \omega \mathrm{t}$
• This shows:
  
  • The flux, and emf oscillate with the same frequency   
  • The flux and the voltage are out of phase by $\pi/2$
  • The induced emf is proportional to the angular frequency. If angular frequency is doubled the peak voltage is also doubled.
    
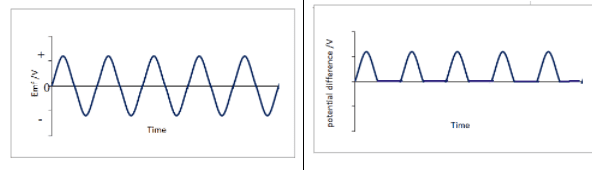
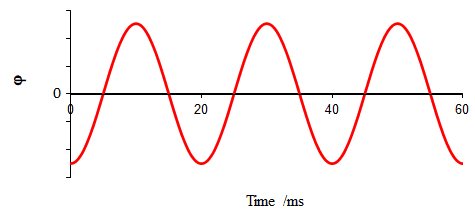
• In the example below, the coil rotates with a period of $\rm 20~ms$.
  
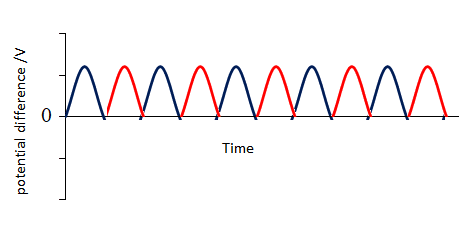
• The corresponding induced emf and current in a domestic supply are shown below.
  
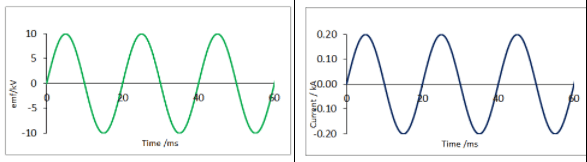
• The following should be noted:
  • The flux, emf and current oscillate with the same frequency.
  • The current and the voltage are in phase
  • When the flux is zero the rate of change of flux has maximum magnitude and so has the emf and current. 
  • When the flux has maximum magnitude the rate of change of flux is zero and so is the emf and current.

• Consider the dc and ac circuits below:
  
  If the bulbs have the same brightness they are working at the same power.
  $\rm P=V_{d c} I_{d c}=V_{a c} I_{a c}$
• In an ac circuit power is not constant in time. It has a maximum value $\rm P_{\max }$ given by the product of the peak voltage and peak current: $\rm P_{\max }=V_{0} I_{0}$ and a minimum value of $0 \mathrm{~V}$.
• The average power $\rm =½ V_{0} I_{0}=V_{a c} I_{a c}$
  • $\rm I_{a c}=\dfrac{1}{\sqrt 2} I_{0}=I_{r m s}$
  • $\rm V_{a c}=\dfrac{1}{\sqrt 2} V_{0}=I_{r m s}$
• The rms current $\rm \left(I_{m m s}\right)$ is the current which in a dc circuit would give the same power dissipation as the average power in the ac circuit.
  The rms voltage $\rm \left(V_{\text {rss }}\right)$ is the voltage which in a dc circuit would give the same power dissipation as the average power in the ac circuit
  In the graphs above:
  • $\rm V_{0}=10.0 \mathrm{kV}$ and $\rm V_{tms}=10.0 / \dfrac{1}{\sqrt{2}} \mathrm{kV}=7.07~ \mathrm{kV}$
  • $\rm I_{0}=0.20 \mathrm{kA}$ and $\rm I_{ms}=\dfrac{1}{\sqrt{2}} 0.20 ~kV=0.14~ \mathrm{kA}$
The resistance $\rm (R)$ of the circuit $=10 / 0.20=7.07 / 0.14=50 \Omega$.
• The average power dissipated in ac circuits can be calculated from rms quantities using the same formula as dc circuits:
  $\rm P_{\text {avcrage }}=V_{\text {rms }} I_{\text {mss }}=V^2{_{rms}} / R=I^2{_{rms}} ~R$
  $\mathrm{rms}=$ root mean square so it is the square root of the mean of the $\mathrm{I}^{2}$ or $\mathrm{V}^{2}$ values.
  It is the most appropriate average to take when the quantity is oscillating in positive and negative directions with a mean of zero.

• Consider two coils: a primary and a secondary with Np and Ns turns of wire respectively
  
• An alternating voltage $\varepsilon p$ is applied to the primary coil which produces a varying magnetic field in the core. This varying magnetic field also passes through the secondary coil. The changing flux linkage induces a secondary emf $\varepsilon$.
  $\varepsilon_{p}=-\rm \Delta \Phi_{p} / \Delta t=-N_{p} \Delta B A / \Delta t$
  $\varepsilon_{p} /\rm N_{p}=-\Delta B A / \Delta t$
  $\varepsilon_{p} / \rm N_{p}=\varepsilon_{S} / N_{S}$
  $\varepsilon_{p} / \rm \varepsilon_{S}=N_{p} / N_{S}$
  ––––––––––––––
  $\rm \varepsilon_{S}=-\Delta \Phi_{s} / \Delta t=-N_{S} \Delta B A / \Delta t$
  $\rm \varepsilon_{S} / N_{S}=-\Delta B A / \Delta t$
• For an ideal transformer with $100 \%$ efficiency the power in the secondary coil equals that in the primary coil and so $\rm \varepsilon_{\mathrm{p}} I_{\mathrm{p}}=\varepsilon_{s} I_{\mathrm{s}}$.
  $\rm \varepsilon_{\mathrm{p}} / \varepsilon_{\mathrm{s}}=I_{\mathrm{s}} / I_{\mathrm{p}}=N_{p} / N_{S}$
  In the example above $\rm N_{p}=3$ and $\rm N_{S}=6$ so
  $\rm \varepsilon_{\mathrm{p}} / \varepsilon_{\mathrm{s}}=I_{\mathrm{s}} / I_{\mathrm{p}}=2$
• Transformers can only be used with alternating current and do not change the frequency of the ac current.
  The symbol for a transformer:

• Power losses with non-ideal transformers include:
  • Heat losses in the resistance of the coils.
  • Losses due to unwanted eddy currents induced in the iron core. These currents can be reduced by laminating the core into individually insulated thin strips.
    
  • Losses due to hysteresis which make the iron core warm up as a result of the continued cycle of changes to its magnetism.
  • Not all magnetic flux produced by the primary coil links with the secondary coil.

• Transformers are used to reduce power losses in cables during the transmission of electricity.
  If the cables have a resistance $\rm (R)$ the power lost $\rm \left(P_{\text {lost }}\right): P_{\text {lost }}=I^{2} R$.
  This loss is minimised if the current is as small as possible.
  As $\rm P=VI$ for a given power transmission $\rm V$ must be large.
• A power station produces a large amount of power; the voltage is stepped up by transformers before transmission and then stepped-down near the place of use to a suitable value before supplying to consumers at suitable smaller voltages.

Worked Example

A power station produces $\rm 800 ~MW$.
Compare the energy losses when this is transmitted at $\rm V_{1}=200 ~kV$ and $\rm V_{2}=50~kV$.

Solution

Stepping the voltage up by a factor of $4$ reduces the power losses by factor by $16$.

• Alternating current(ac) is the easiest to generate, transform and transmit but direct current (dc) is needed for many electrical devices.  
• The conversion from ac into dc is called rectification which uses diodes.
  An ideal diode allows current to flow in only one direction.
• It has negligible resistance in the forward direction and infinite resistance in the reverse direction.

The potential difference-current graph for a diode

The symbol for a diode:

Consider the circuit below:

• The graph of the emf produced by the ac source and the potential difference across the resistor are shown.
  
• This half-wave rectification produced by a single diode converts ac into a pulsating dc current.
  The electrical energy in the negative cycle of the ac is not available for use.

• A diode bridge of four diodes uses all the electrical energy that is available during a complete cycle.
  
• The current always passes through the resistor in the same direction for an alternating source.
• In one half of the half of the cycle, current flows in the direction of the blue arrows and in the other half in the direction of the red arrows.
  
• The voltage across the resistor varies as follows. This is full wave rectification.
  
• The following points should be noted:
  • Diodes on parallel sides point in the same directions.
  • Diodes point in opposite directions at the junction where the $\rm AC$ current enters and leaves the bridge.
    Only two diodes conduct during each half-cycle
• The output of the diode bridge rectifier can be made smoother by adding a capacitor in parallel to the load. This is covered in more detail in section $11.3$.