Oscillations occur in many areas of physics with simple harmonic motion (shm) a special case of oscillation that appears in various natural phenomena.
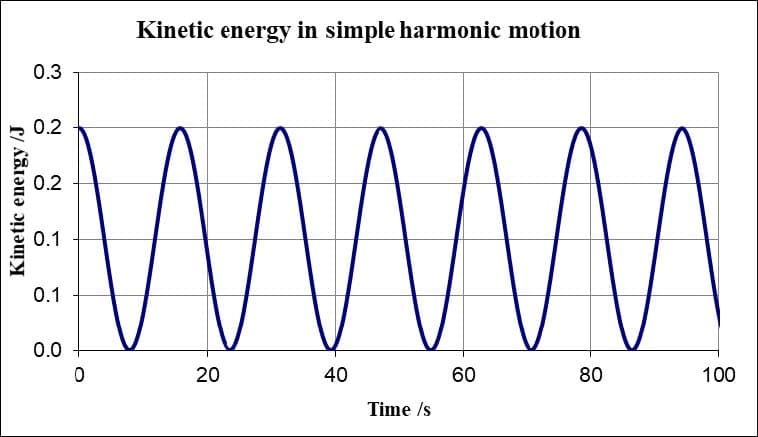
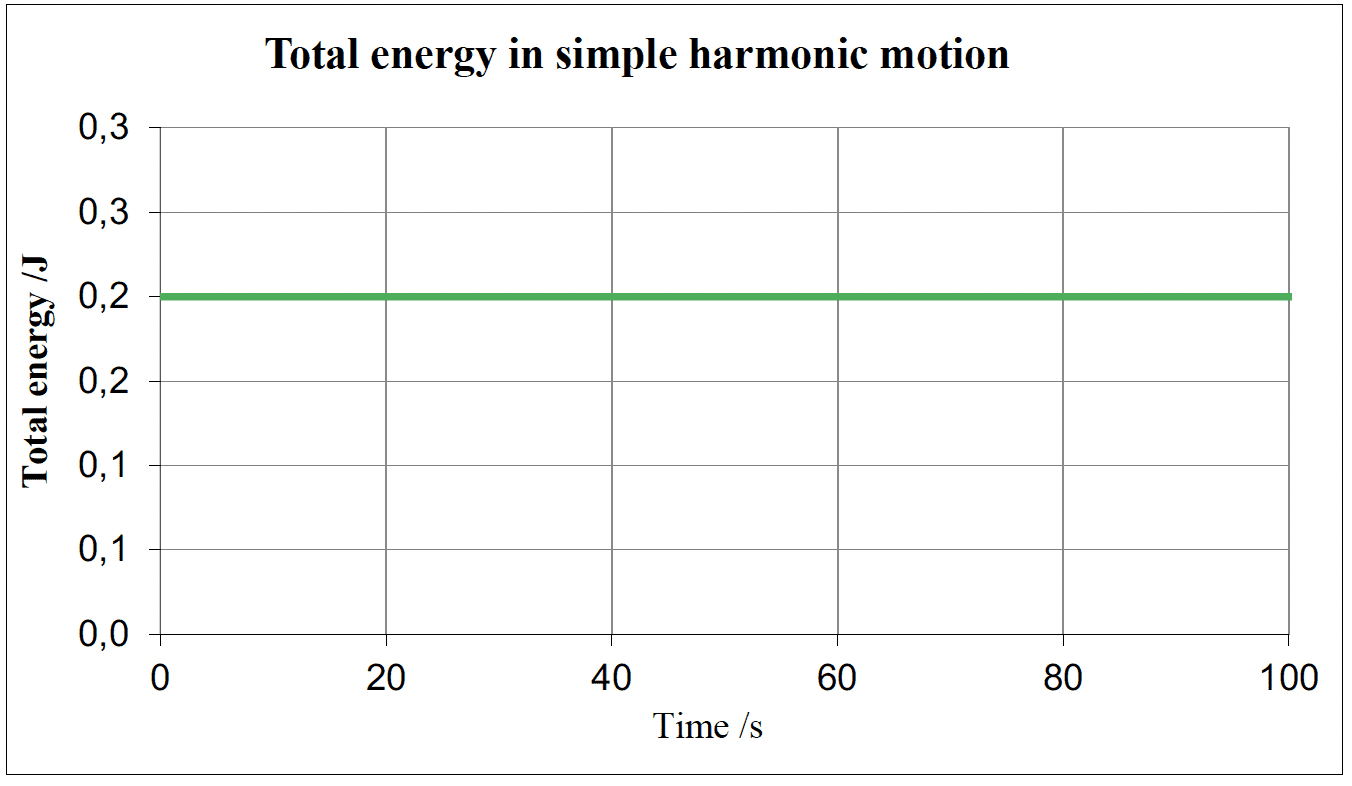
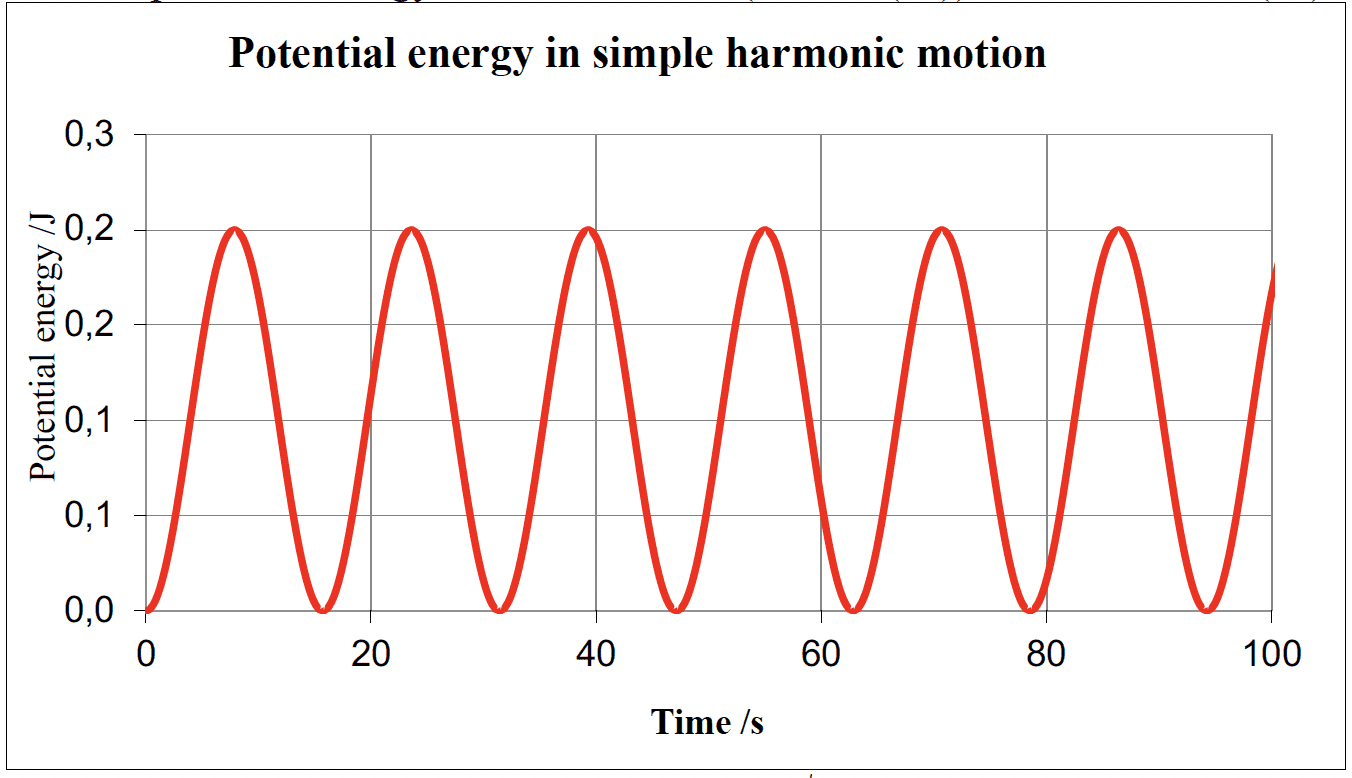
- Oscillations involve the interchange between kinetic and potential of energy.
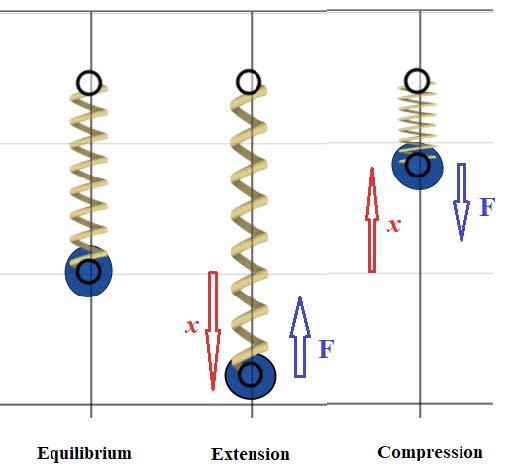
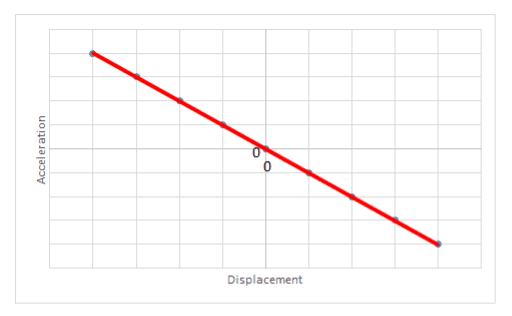
- In Simple harmonic motion (SHM) the acceleration is proportional to the displacement from equilibrium but in the opposite direction:
$a = −\omega^2x$ where $\omega$ is the angular frequency. $\omega$ has units of rad per second. - This acceleration is caused by a restoring force that is always directed towards the mean position and is also proportional to the displacement from that mean position.
- Displacement is a vector quantity which measures the position of a point relative to its equilibrium position.
- The maximum displacement is called the amplitude.
- SHM consists of periodic oscillations with a period $\rm (T)$ that is independent of the amplitude: $\rm T = 2\pi/\omega$
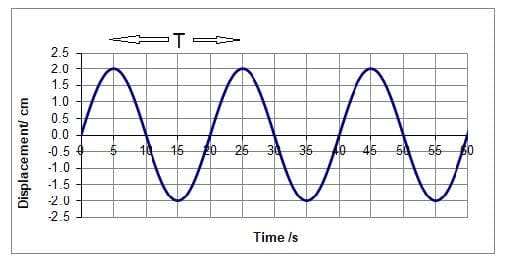
In this example $\rm T = 20~s$ and the amplitude $\rm = 2.0~cm$. - The frequency $(f)$ of an oscillation is the number of cycles per second. $f= 1/\rm T$
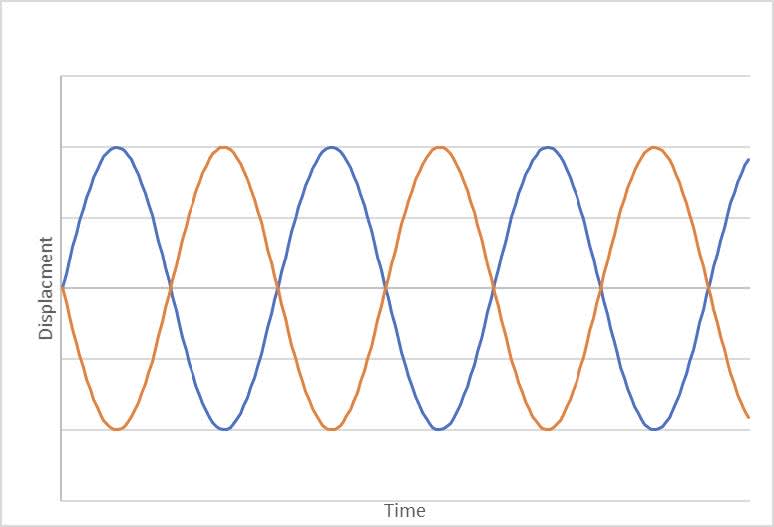
As $\mathrm T = 1/f =2\pi/\omega$. This gives $\omega = 2\pi f$ - The displacement can be described by a sin or cos curve depending on the initial displacement.
For example, with an initial displacement of $0$, an amplitude $0 =1$ and $\omega=0.20$:
For this curve $\rm T = 2\pi/\omega$ $= 2\pi/0.2$ $= 10 \pi$ $\rm = 31.4~s$$x = x_0\sin \omega t$ 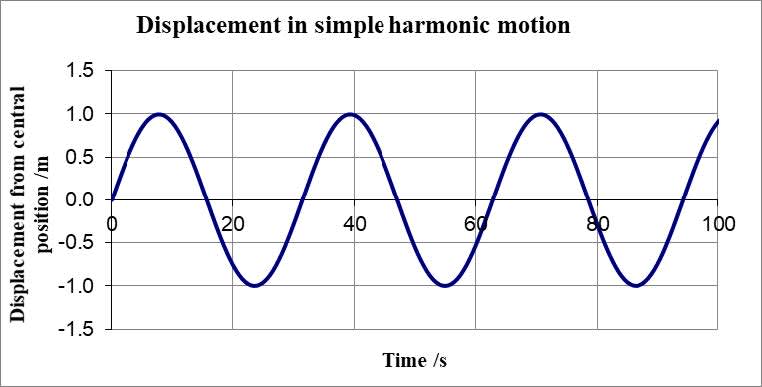
- The velocity can be determined from the slope of the displacement-time graph. In this example it is a maximum at $t = 0$ and so follows a cosine curve.
It should be noted that $v_0 = 0.20 = \omega x_0 = 0.2 \times 1.0$$v = v_0 \cos\omega t$
Note:
$v_0 = 0.20$
$v = \omega x_0\cos\omega t$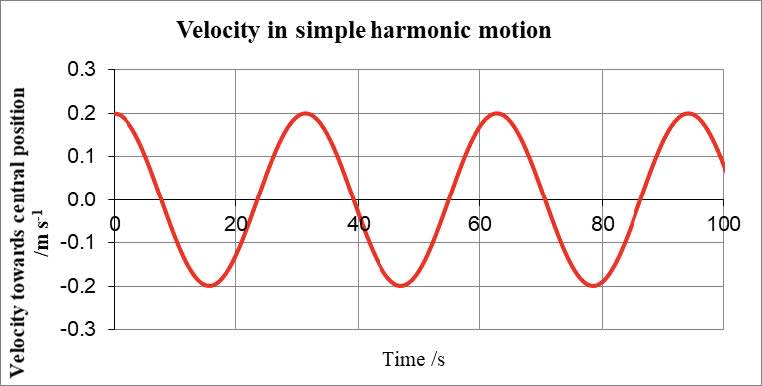
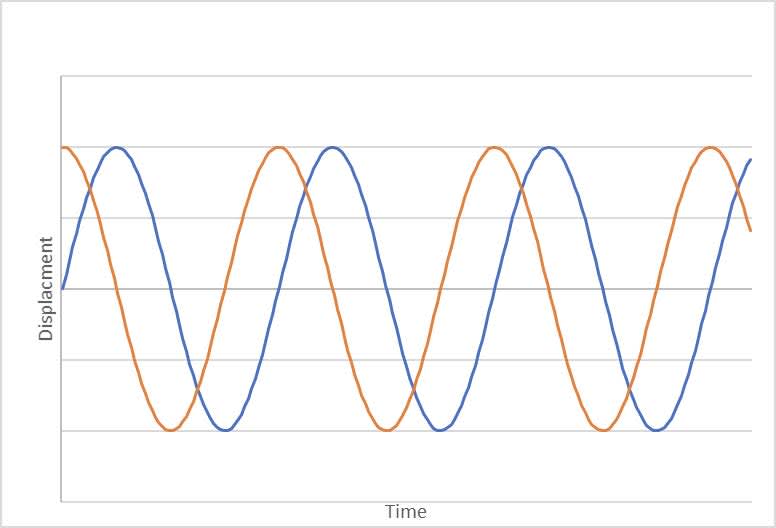
- The acceleration can be determined from slope of the velocity-time graph.
- In this example it is a minimum at $t = 0$ and so follows a -sin curve.
It should be noted that $a_0 = 0.04 = 0.20^2 \times 1.0 = \omega^2 x_0$$a = -a_0\sin\omega t$
Note:
$a_0 = 0.04$
$a = -\omega^2 x_0 \sin\omega t$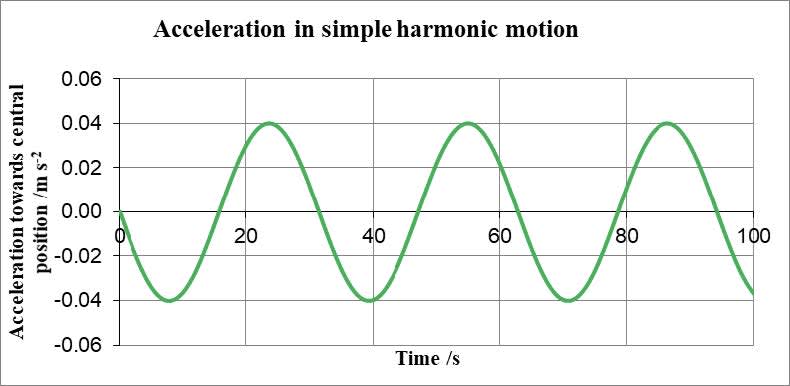
 Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA