Nuclear reactions

Energy can be released in nuclear reactions as mass is converted to energy.

• A nucleus with $\rm Z$ protons and $\rm N$ neutrons has a mass that is less than the sum of the mass of the protons and neutrons. The mass defect $(\Delta_{\text {mass defect }})$ is this difference.
  $\rm\Delta mass_{defect}=\mathcal n_{proton}\times \mathcal m_{proton}$ $+$ $\rm \mathcal n_{neutron} \times \mathcal m_{neutron} - M_{nucleus}$
  $\rm \Delta mass_{defect} = Z \times \mathcal m_{proton} + (A - Z) \mathcal m_{neutron} - M_{nucleus}$
• The mass is reduced as energy is given out as the nucleus is formed. The binding energy is the amount of energy released. It is also the minimum energy needed to reverse this process and separate a nucleus into its individual nucleons.
  $$
  \Delta \rm E_{BE} = \Delta mass_{defect} ~\mathcal c^{2}
  $$
• A graph of the binding energy per nucleon against nucleon number $A$ shows a peak around the nuclei $\mathrm{Fe}-56 / \mathrm{Ni}-62$. These are the most stable nuclei.
  

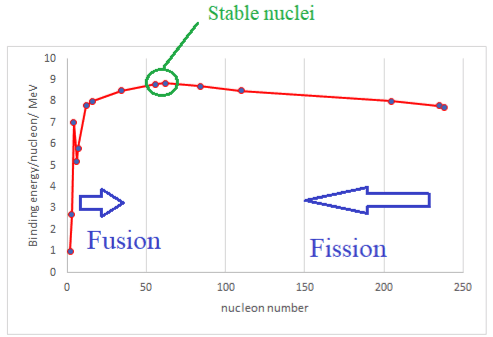
• Most nuclei have approximately the same binding energy per nucleon of $\rm 8.5~ MeV$. This similarity in binding energy per nucleon is due to the short range of the strong nuclear force: in a large nucleus any one nucleon is surrounded by the same number of nucleons and so it takes the same energy to remove it.

• A nuclei reaction is energetically feasible if the products of the reaction have a greater binding energy per nucleon when compared to the reactants. Small nuclei undergo fusion reactions and large nuclei undergo fission reactions.
• In a fusion reaction two light nuclei combine together (fuse) to form a heavier nucleus plus energy. For example two deuterium nuclei (isotopes of hydrogen) produce helium$-3$ (an isotope of helium) and a neutron:
  $$
  ^2_1 \mathrm{H}+^2_1 \mathrm{H} \rightarrow ^3_2 \mathrm{He}+^1_0 \mathcal{n}
  $$
• In a fission reaction a large nucleus splits (fissions) into two smaller nuclei with some neutrons and gives out energy (and usually photons). For example a neutron is absorbed by a nucleus of uranium$- 235$, uranium momentarily turns into uranium$-236$ which then splits into lighter nuclei plus neutrons.
  $^1_0n +^{235}_{92} \mathrm{U} \rightarrow ^{236}_{92} \mathrm{U} \rightarrow ^{144}_{56} \mathrm{Ba}+^{89}_{36} \mathrm{Kr}+3^1_0 n$
• When an element is induced to change it is an artificial transmutation reaction.
• As mass and energy can be interconverted it is often useful to express the unified mass unit in units of energy.
  $$
  1 \mathrm{u}=931.5 ~\mathrm{MeV} / c^{2}
  $$

First Worked Example

Calculate the energy in $\mathrm{MeV}$ released in the nuclear fusion reaction:
$$
^2_1 \mathrm{H}+^2_1 \mathrm{H} \rightarrow ^3_2 \mathrm{He}+^1_0 n
$$

using the following data.

Solution

From the mass difference we can work out the energy released:
$\Delta m=2 \times 2.014102-(\scriptstyle{3.016029~+~1.008665}$$) \mathrm{u}$
$\Delta m=0.0035 \mathrm{u} \Delta \rm E$ $=\Delta m c^{2}=0.0035 \times 931.5=3.26~ \mathrm{MeV}
$

Second Worked Example

Calculate the energy in MeV released in the nuclear fission reaction from the following data.
$$\rm ^{236}_{92}U \rightarrow ^{144}_{56}Ba + ^{89}{36}Kr + 3^1_0\mathcal n$$

$$1 \mathrm{u}=931.5 \mathrm{MeV} / c^{2}$$

Solution

$\Delta m=(143.92292+88.91781$ $+$ $3 \times 1.008665) \mathrm{u}-236.0526 \mathrm{u}$ $=0.185875 \mathrm{u}$
$\Delta \mathrm E=\Delta m c^{2}=0.185875 \times 931.5 \approx 173 \mathrm{MeV}$
This energy appears as kinetic energy of the products.