Nuclear physics

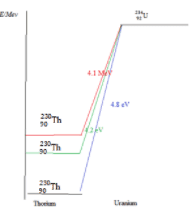
The nucleus occupies discrete energy levels like the electron. 

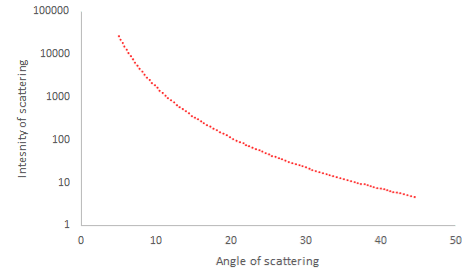
• Evidence of the size of the nucleus can be obtained by firing alpha particles at a nucleus
• For a given speed of an alpha particle, the closest approach to a nucleus, $r_{\min}$ will occur when the initial kinetic energy has been converted into electric potential energy.
  
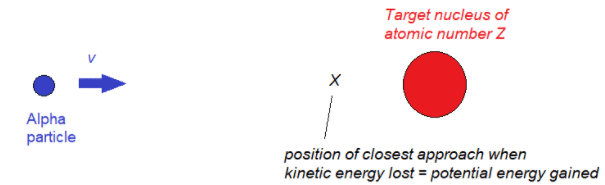
  Kinetic energy lost $=½~ m v^{2}$
  Potential energy gained $=\mathrm Q q / 4 \pi \epsilon_{a} r$
  $\mathrm{Q}$ is the charge of target nuclei $\mathrm{Ze}$ and $q$ is the charge of an alpha particle $=2 \mathrm{e}$
  Potential energy gained $\rm =2 e \times Z e / 4 \pi \epsilon_{o} \mathcal r$ $=\rm Z e^{2} / 2 \pi \epsilon_{o} \mathcal r$
  At the position of closest approach:
  $½~ m v^{2}=\rm Z e^{2} / 2 \pi \epsilon_{o} \mathcal r_{\text {min }}$
  $r_{\min }=\rm Ze^{2} / 2 \pi \epsilon_{0} \mathcal{m v}^{2}$

Worked Example

Calculate the diameter of a gold nucleus $\rm (Z=79)$ if an alpha particle with a kinetic energy of $2.0 \mathrm{MeV}$ is scattered backwards.

Solution

$\rm E_{k}=2.0 \times 10^{6} \times 1.6 \times 10^{-19} ~J$
$m v^{2}=2 \times 2.0 \times 10^{6} \times 1.6 \times 10^{-19} \mathrm{~J}$ $=4.0 \times 10^{6} \times 1.6 \times 10^{-19} \mathrm{~J}$
$r_{\min }= 79 \times(1.6 \times 10^{-19})^{2} /(2 \pi \times 8.85$ $\times$ $10^{-12} \times 4.0 \times 10^{6} \times~ 1.6 ~\times~ 10^{-19}) \mathrm{~J}$
$r_{\min }=5.68282 \times 10^{-14}$
$d=2 \times 5.68282 \times 10^{-14}$
$d=1.1 \times 10^{-13} \mathrm{~m} .$

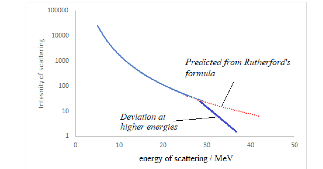
• This distance gives an overestimate for the diameter of a nucleus. It is outside the range of the nuclear force, so the alpha particle is simply repelled by the electrostatic repulsive force.
• If the energy of the incoming particle is increased, the distance of closest approach decreases allowing a better estimate for the nuclear radius.

Deviations

• Rutherford derived a theoretical formula for the scattering of alpha particles from nuclei. The Rutherford formula states that as the scattering angle $\theta$ increases, the number of alpha particles scattered decreases very sharply. More precisely the number $\mathrm{N}$ of alpha particles is given by $\mathrm N=k / \sin ^{4}(\theta / 2)$
  
• The derivation of the Rutherford formula is based on the assumption that only electrostatic forces need to be considered during the scattering process as outlined in the worked example on gold.
• As the energy of the alpha particles increases, the alpha particles can get closer to the nucleus and at a distance of about $\rm 10^{-15} ~m$ deviations from the Rutherford formula are observed. The alpha particles are so close to the nucleus that the strong nuclear force, not included in the Rutherford model, begins to act on the alpha particles.
  
• The presence of these deviations from perfect Rutherford scattering is evidence for the existence of the strong nuclear force.

• The nuclear radii can also be determined by sending beams of neutrons or electrons at nuclei. If the de Broglie wavelength $\lambda$ of the electrons or neutrons is about the same as that of the nuclear diameter, the electrons and neutrons will diffract around the nuclei.
• From Topic 9 a minimum will be formed at an angle $\theta$ to the original direction when sin $\theta \approx \lambda/b$
  $b$ is the diameter of the diffracting object, in this case the nucleus.
• Electrons probe the nuclear charge distribution as the strong force does not act upon them.
• Neutrons can approach very close to the nucleus as they have no charge and are not repelled by an electrostatic force. 

Worked Example 

A beam of neutrons of energy $85~ \mathrm{MeV}$ is incident on a lead foil. Estimate the radius of a lead nucleus if the first diffraction minimum is observed at an angle of $13°$ relative to the central beam.
The mass of a neutron is $m=1.67 \times 10^{-27} \mathrm{~kg}$

Solution

$\sin \theta \approx \lambda b$ ($\lambda$ is the de Broglie wavelength of the neutron).
The mass of a neutron is $\rm m=1.67 \times 10^{-27} \mathrm{~kg}$ and its kinetic energy is $85~ \mathrm{MeV}$, the wavelength is $\lambda=h / p$
$p^{2} / 2 m=\mathrm E_{k}$
$p=\sqrt{2} \mathrm E_{k} \rm m$
$p=\sqrt{2} \times 85 \times 10^{6} \times 1.6 \times 10^{-19}$ $\times$ $1.67 \times 10^{-27}$
$p=2.13 \times 10^{-19} \mathrm{Ns}$
$\lambda=h p=6.63 \times 10^{-34} / 2.13 \times 10^{-19}$
$\lambda=3.1 \times 10^{-15} \mathrm{~m}$
Therefore the diameter of the nucleus is given by:
$b=\lambda / \sin 13^{\circ}=3.1 \times 10^{-15} / \sin 13°$
$b=14 \times 10^{-15} \mathrm{~m}$
This corresponds to a radius of $7 \times 10^{-15} \mathrm{~m}$.

Experiments show the nuclear radius $R$ depends on mass number $A$ according to the expression: $\rm R=R_{0} A^{1 / 3}$ where $\rm R_{0}=1.2 \times 10^{-15} \mathrm{~m}=1.2 \mathrm{fm}$.
This expression implies that all nuclei have the same density:
$\rm V_{\text {nucleus }}=4 \pi / 3 R^{3}$ substituting for $\rm R=R_{0} A^{1 / 3}$
$\rm V_{\text {nucleus }}=4 \pi / 3\left(1.2 \times 10^{-15} \times A^{1 / 3}\right)^{3}$
$\rm V=7.24 \times 10^{-45} \times A \mathrm{~m}^{3}$
The mass of the nucleus is $\rm A$ u, i.e. $\rm A \times 1.66 \times 10^{-27} \mathrm{~kg}$.
$\rm density (\rho)= mass / volume$ $=\rm A \times 1.66 \times 10^{-27} / 7.24 \times 10^{-45} \times A$
As the $\rm A$ cancels out: $\rho \approx 2.3 \times 10^{17} \mathrm{~kg} \mathrm{~m}^{-3}$
And all nuclei have the same density
This is not surprising as all nuclei are composed of protons and neutrons packed closely together.

• We saw earlier that the photons emitted from atoms have discrete energy as the electron energy levels are quantised.  Similarly, the discrete energies of alpha and gamma particles produced in radioactive decay are evidence for nuclear energy levels. The protons and neutrons in a nucleus exist in discrete energy levels just as the electrons in atoms do. In a transition from one energy level to a lower one the emitted alpha or gamma particles have the discrete energy that is the difference in energy between the levels involved.
• Note in beta decay the electron/positrons are emitted have a continuous range of energies as explained later.
• An example of nuclear energy levels: Alpha Decay from uranium-234: $\rm ^{234}_{92}U \rightarrow ^{230}_{90} Th+^4_2He$
  The alpha particles are emitted with discrete energies of:
  $4.1 ~\mathrm{MeV}$,
  $4.2 ~\mathrm{MeV}$ and $4.8 \mathrm{MeV}$,
  which implies that the thorium is produced in three different energy levels.
  

• The continuous range of energies produced in beta minus decay is evidence for the antineutrino. The discrete energy available is shared in many different ways depending on their direction of motion. Although the total energy change is fixed there are an infinite number of ways of sharing this between two particles.
• Similarly, the neutrino shares the energy with a positron in beta plus decay.

• The law of radioactive decay states that the rate of decay is proportional to the number of nuclei present that have not yet decayed: $\mathrm {dN} / \mathrm d t =-\lambda \rm N$
  The constant of proportionality, $\lambda$ is the decay constant.
• The probability that any one nucleus decays is:
  probability $=-\mathrm{d N} / \mathrm N=\lambda \mathrm{d} t$
  The probability of decay per unit time $=$ probability/ $\mathrm{d} t=\lambda$
  The decay constant λ is the probability of decay per unit time.

$\mathrm{d N / d} t=-\lambda \rm N$
$\mathrm{d N / N =-\lambda d} t$

Integrating this equation to give the variation of $\mathrm{N}$ with time.
$\ln \mathrm N = -\lambda t+\ln$
$\rm N_{0}$ is the number of nuclei at time $t=0$
$\rm \ln N / N_{0}=-\lambda t$
Expressing this equation in exponential form.
$\mathrm{N / N_{0}}=\mathrm{e}^{-\lambda t}$
The number of nuclei of the decaying element decreases exponentially with time as discussed in Topic 7.

The half-life $\left(t_{½}\right)$ is the time for $\mathrm{N}$ to fall to $½\rm N_{0}$.

$\ln ½ \mathrm{N_{0} / N_{0}}=-\lambda t_{1 / 2}$
$\ln ½ =-\lambda t_{2 /3}$
$\ln 2=\lambda t_{¼}$
$\rm \lambda=\ln 2 / t_{½}$

The (negative) rate of decay (i.e. the number of decays per second) is called activity $\rm (A)$: $\mathrm A=-\mathrm{d N} / \mathrm{d} t=\lambda \rm N$
It follows from the exponential decay law that activity also satisfies an exponential law:
$\mathrm{N=N_{0} \mathrm{e}}^{-\lambda t}$
$\mathrm{A=-d N / d} t=\lambda \mathrm{N_{0} e}-\lambda t \quad \lambda\rm N_{0}=A_{0}$
$\mathrm{A=A_{0} e}-\lambda t$
After one half-life, $\rm T_{½}$, half of the nuclei present have decayed and the activity has been reduced to half its initial value.
The unit of activity is the becquerel: $1 \mathrm{~Bq}=1$ decay per second.

Worked Example 

Determine the decay constant for the nuclide shown in the graph.

Solution
Time for the activity to fall from $500 \mathrm{~Bq}$ to $250 \mathrm{~Bq}=4 \mathrm{~s}$
$\lambda=\ln 2 / 4 \mathrm{~s}-0.173 \mathrm{~s}^{-1}$