Newton’s idea of gravitational force acting between two spherical bodies and the laws of mechanics allows us to predict the planets.
- Two point masses $\rm m_{1}, m_{2}$ separated by a distance $\rm r$ attract each other with a force $\rm F$ :
- $\rm F=G m_{1} m_{2} / r ^{2}$
The forces experienced by the bodies are equal and opposite - an example of Newton's third law.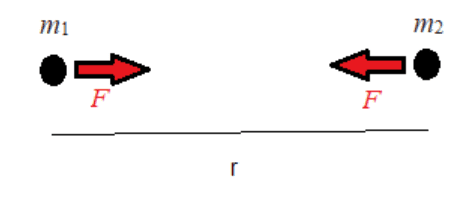
$\rm G$ is the universal gravitational constant: $\rm G=6.67 \times 10^{-11} N m ^{2} kg ^{-2}$. - The equation can also be used for two uniform spherical masses, with a centre-to-centre separation $r$.
- The similarities with Coulomb's electrostatic law should be noticed. They are both inverse square laws. The electrical law can be attractive or repulsive, but the gravitational force is always attractive.
- A body of mass $\rm M$ creates a gravitational field in the space around it. This field acts on other bodies by exerting a gravitational force.
|
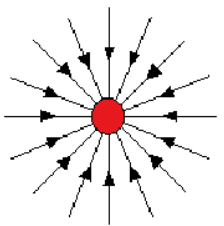 |
- The gravitational field strength $\rm (g)$ at a point is the gravitational force per unit mass exerted on a small, mass $\rm m$ placed at that point. It is a vector quantity.
For a mass $\rm M$:
$\rm g= F / m=G M m / m r^{2}$ $\rm =G M / r^{2}$ - The gravitational field strength at the surface of a planet is the same as the acceleration due to gravity on the surface.
Consider a mass $\rm m$ at the surface of a planet of mass $\rm M$ and radius $\rm R$ :
$\rm F=G M m / R^{2}=m g=m a$
$\rm a=g=\rm G M / R^{2}$
It should be note that $\rm N = kg.ms ^{-2}$ $(\rm F = ma )$
$\rm N. kg ^{-1}= ms ^{-2}$ - Satellites and planets are kept in approximate circular paths by gravitational forces which provide the necessary centripetal force.
$\rm F=G M m / r^{2}=m v^{2} / r$
$\rm GM / r =v^{2}$
As $\rm v=2 \pi r / \rm T$
where $\rm T$ is the period,
We can deduce Kepler's third law:
$\rm v^{2}=4 \pi^{2} r^{2} / T^{2}=G M / r$
$\rm T^{2}=\left(4 \pi^{2} / G M\right) r^{3}$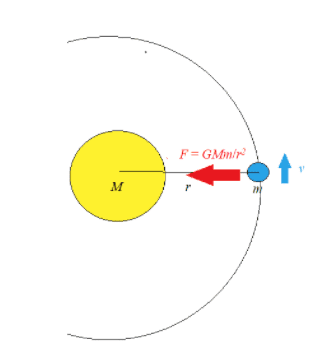
 Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
