Motion

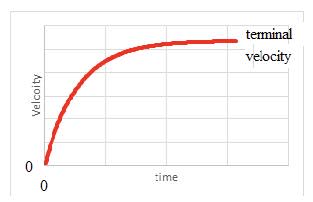
Motion may be described and analysed by the use of graphs and equations.

• Speed and distance are scalar quantities.
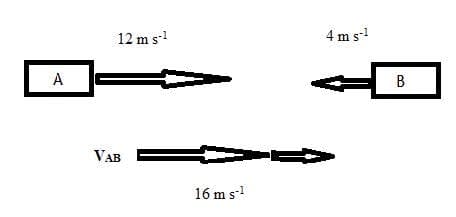
  Average speed $=$ total distance travelled $(d)$ / total time taken $(t) = d/t$
• Displacement and velocity are vector quantities.
  Displacement is the distance from a fixed point in a given direction.
  Average velocity $=$ change of the displacement(s) / total time taken $(\Delta t) = \Delta s/\Delta t$
  The average velocity vector is in the same direction as $\Delta s$.
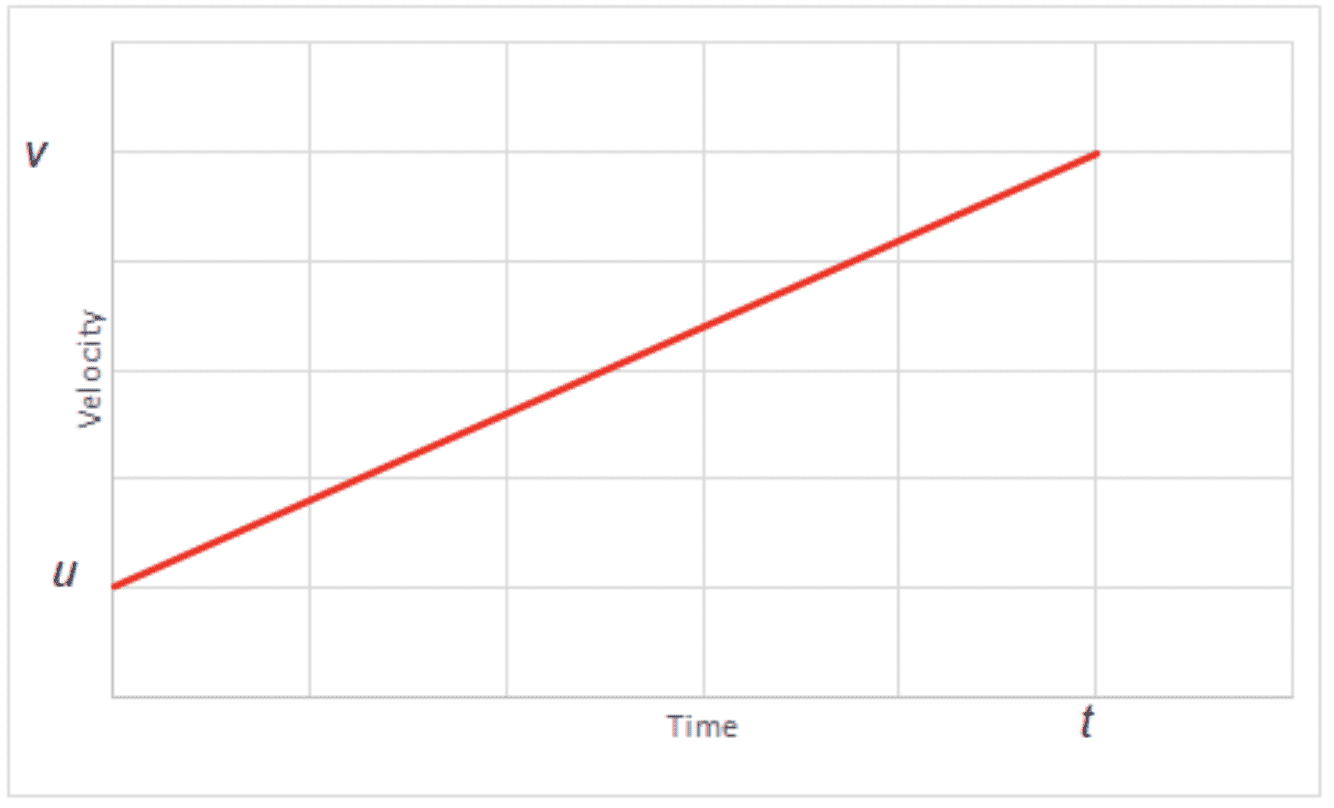
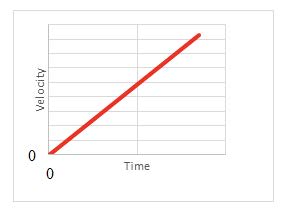
  Consider a body undergoing constant velocity.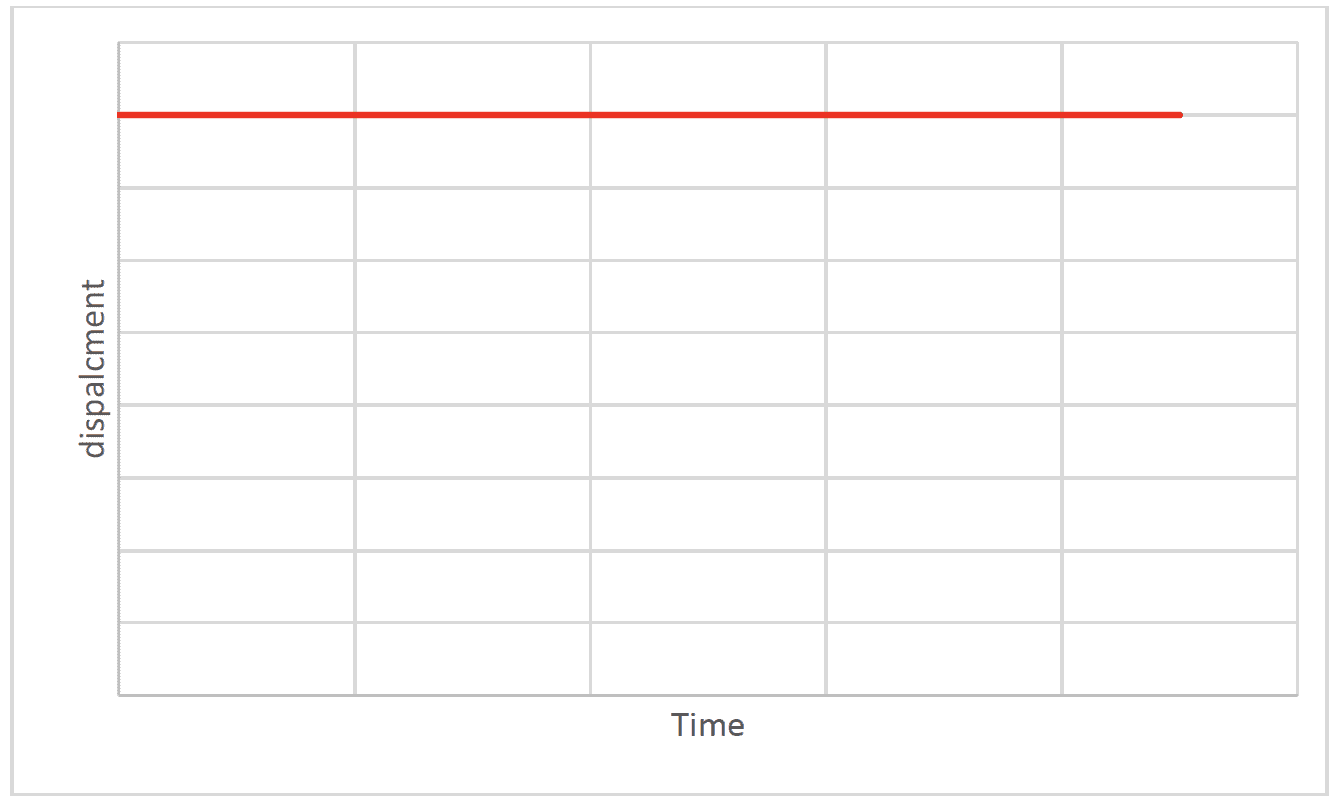
  
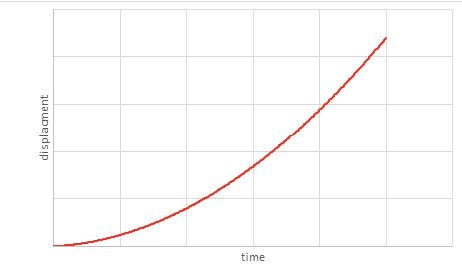
  The gradient of the displacement–time graph gives the velocity. This s a general result.
• Instantaneous speed and velocity are the speed and velocity at a specific time. They can be thought of as the average determined in the period $t$ to $t + \Delta t$ where $\Delta t$ is almost zero. They are generally determined from the tangent of the distance / time or displacement/time graphs.
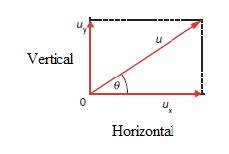
• Acceleration is a vector quantity.
  Average acceleration $=$ change of velocity vector $(\Delta v)$ / total time taken $(\Delta t) = \Delta v / \Delta t$
  The average Acceleration vector is in the same direction as $\Delta v$.
• Instantaneous acceleration is the acceleration at a specific time. It can be thought of as the average determined in the period $t$ to $t + \Delta t$ where Δt is almost zero. It can be y determined from the tangent of the velocity / time graph.

• Consider the motion of an object from an initial velocity $u$ and a final velocity $v$ during a time $t$ with constant acceleration $a$.
• Average velocity $= (u + v) / 2$
• Displacement $(s) = (u + v) t / 2$
  Note this is the area under the graph. This is general result:
  Displacement $=$ area under the velocity time graph.
• Acceleration $(a) = (v - u) / t$
  Note this is the slope of the graph. This is general result:
  Acceleration is the gradient of the velocity time graph.
• These equations lead to the $suvat$ equations:
  $v = u + at$
  $s = (u + v)t / 2$
  $s = ut + ½ at^2$
  $v^2 = u^2 + 2as$
  The corresponding displacement and acceleration graphs for constant acceleration.
  
• The area under the acceleration time graph $= at = v - u$
  This is general result:
  Change of velocity $=$ area under the acceleration $-$ time graph.

Relative velocity of $\rm A$ compared to $\rm B : V_{AB}$

• An important example of uniformly accelerated motion is the vertical motion of an object near the surface of the earth. In the absence air resistance, this is known as free-fall.
• The acceleration due to gravity in the absence air resistance is $\rm 9.81~m ~s^{-2} = 10 ~m ~s^{-2}$. This is often represented as $g$.

The horizontal and vertical motion are independent.

The horizontal component of the velocity remains constant $u_x$ in the absence if air resistance.

The vertical component has uniform acceleration $(g)$ in the absence of air resistance.

• When an object moves through a fluid (a liquid or a gas), there will be a frictional fluid resistance force that opposes the object’s motion. This also effects projectile motion through the air.
• When objects fall the acceleration generally decrease until terminal velocity is reached.
  
• For projectile motion air resistance reduces the vertical and the horizontal components of velocity. This reduces the maximum height and the maximum range. This makes the angle of descent steeper and distorts the shape from a parabolic.

Projectile motion with and without air resistance