Modelling a gas

The properties of ideal gases allow scientists to make predictions of the behaviour of real gases.

Boyle’s law

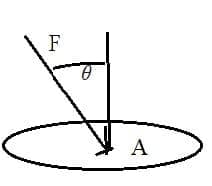
• Pressure $(\mathrm{P})=$ force $\rm (F)$ per unit area $\rm (A)$
  $\rm P=F / A$
  The Unit: $\mathrm{N} \mathrm{m}^{-2}$ or pascal $(\mathrm{Pa})$
• As gas pressure acts equally in all directions there is no resultant pressure in any direction: it is a scalar property.
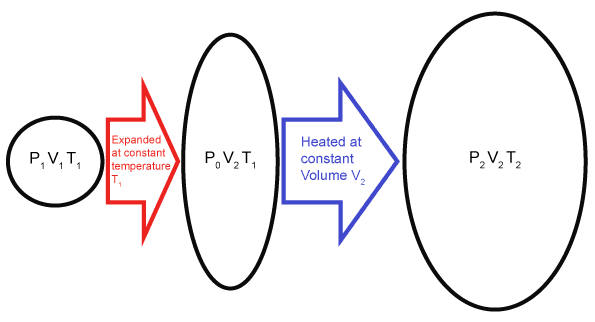
• The pressure of a fixed mass of gas at constant temperature is inversely proportional
  to its volume:
  $\rm P \propto 1 / V$
  $\rm P= \mathcal k / V$ where $k$ is a constant that depends on the amount and temperature of the gas
  $\rm P V=\cal k$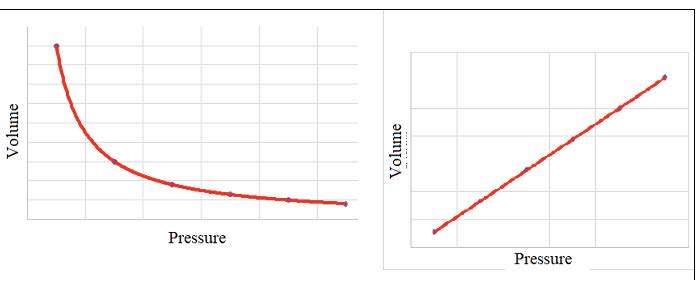
  
  
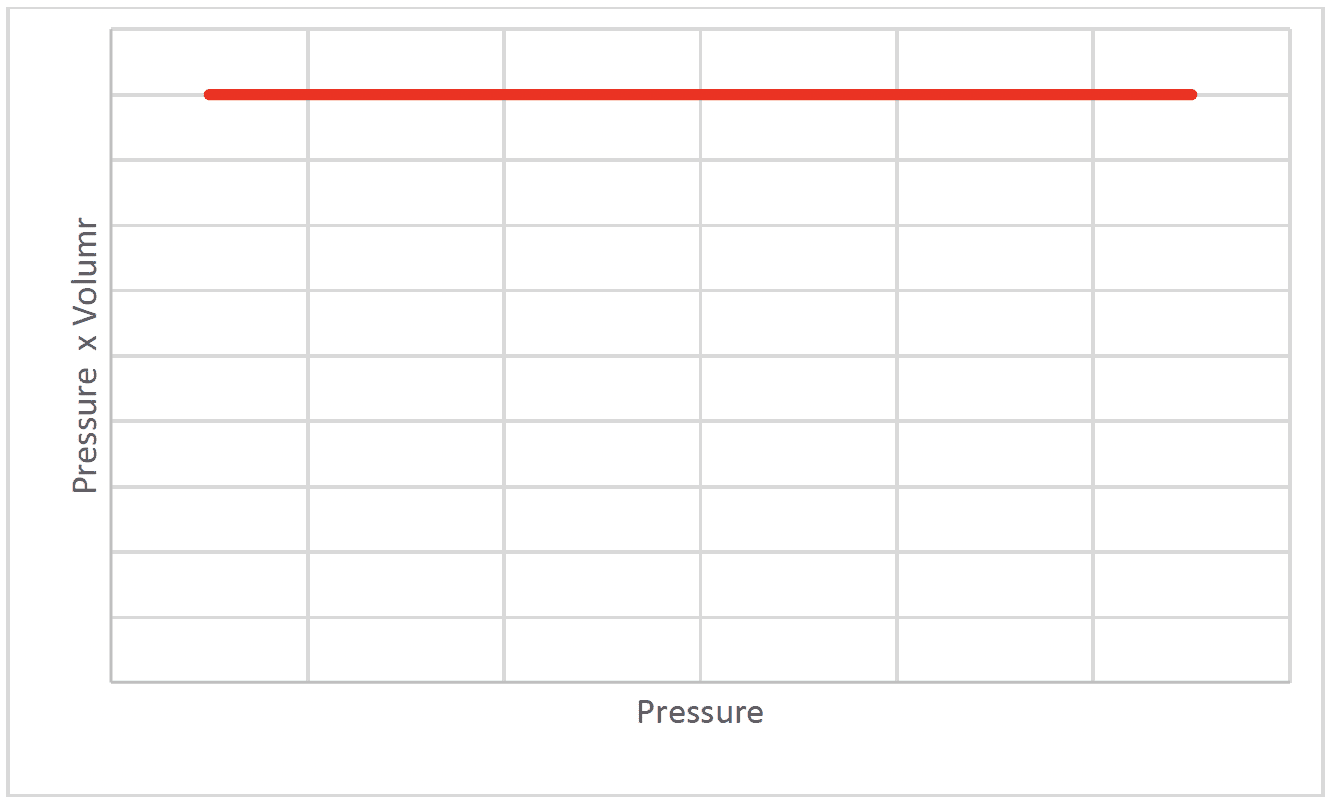
  If the volume of a gas decreases the particles will collide with the walls more often and the pressure increases.

Pressure law

• The pressure of a fixed mass of gas with constant volume is directly proportional to its temperature in kelvin.
• Increasing temperature increases the average $\mathrm E_k$ of the molecules. Molecules collide with the walls more frequently and with more momentum.
  
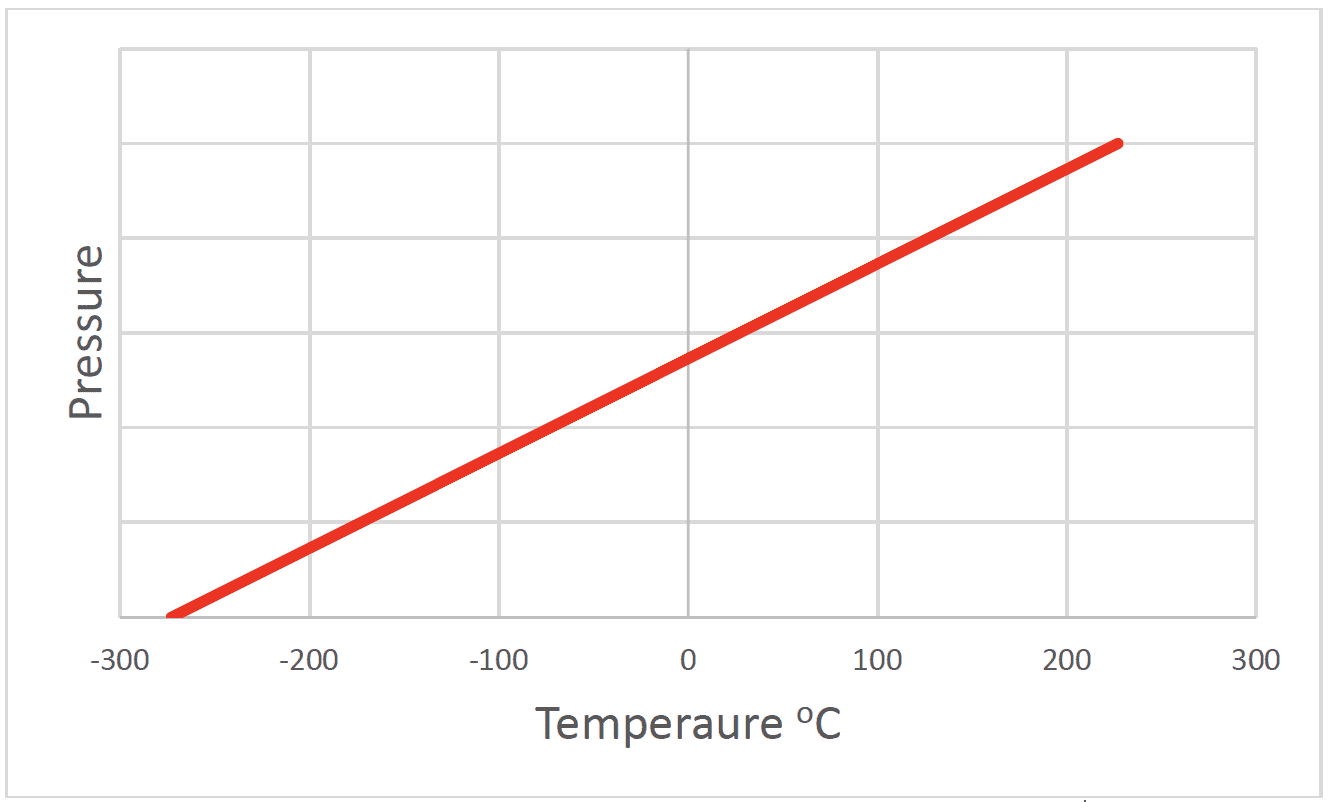
  The pressure of a gas is $0$ at $\rm 273°C$. This is absolute zero $\rm 0~K$.

Charles’ law

• The volume of a fixed mass of gas at a constant pressure is directly proportional to its temperature in kelvin.
  $\mathbf{V} \propto \mathbf{T}(\mathbf{K})$
  An increase in temperature causes the particles to move faster. The pressure is constant if the volume increases, and the particles collide less frequently.

A sample of gas at pressure $\rm P_{1}$, volume, $\rm V_{1}$ and Temperature $\rm T_{1}(K)$ is expanded to a new Volume $\mathrm{V}_{2}$ at constant temperature $\mathrm{T}_{1}$. The new pressure is $\mathrm{P}_{0}$.

a). State the relationship between the pressure $\rm P_{1}$, $\rm V_{1}$ and $\rm P_{0}$, $\mathrm V_{2}$ for expansion at constant temperature $\rm T_{1}$.

$\rm P V= constant$
$\rm P_{1} V_{2}=P_{0} V_{2}$

b). The gas is then heated at constant volume $\rm V_{2}$ to new conditions $\rm P_{2}, V_{2}$, and $\rm T_{2}$.

State the relationship between the pressure $\rm P_{0}$, $\rm T_{1}$ and $\rm P_{2}$, $\rm T_{2}$ when the gas is heated at constant volume $\rm V_{2}$.
$\rm P / T= constant$
$\rm P_{0} / T_{1}=P_{2} / T_{2}$

c). Deduce a relationship between the initial conditions $\rm P_{1}$, $\rm V_{1}$ and $\rm T_{1}$ and the final conditions:

$\rm P_{2}$, $\rm V_{2}$ and $\rm T_{2}$.
From a).
$\rm P_{1}$ $\rm V_{1}=P_{0} V_{2}$
$\rm P_{0}=\left(P_{1} V_{1}\right) / V_{2}$
From b).
$\rm P_{0}=P_{2} T_{1} / T_{2}$
$\rm \left(P_{1} V_{1}\right) / V_{2}=P_{2} T_{1} / T_{2}$
$\rm P_{1} V_{1} / T_{1}=P_{2} V_{2} / T_{2}$

These three laws can be combined in one equation.

$\mathrm{P}_{1} \mathrm{~V}_{1} / \mathrm{T}_{1}=\mathrm{P}_{2} \mathrm{~V}_{2} / \mathrm{T}_{2}=\mathrm{K}$

$\rm K$ only depends on the amount of gas present.

• The amount of substance $(n)$ is measured in moles $\rm (mol)$.
• The mole concept applies to all species: atoms, molecules, ions, and electrons.
• $\rm 1~ mol$ contains $6.02 \times 10^{23}$ particles.
• $6.02 \times 10^{23} \mathrm{~mol}^{-1}$ is called Avogadro's constant $\left(\mathrm N_{a v}\right)$. It has units $\left(\mathrm{mol}^{-1}\right)$ as it is the number of particles per mole.
• $\mathrm{N}$ (number of particles) $=\mathrm{n}(\mathrm{mol}) \times$ Avogadro's constant $\left(\mathrm N_{a v}\right)$ $\mathrm{N}=\mathrm{n} \times \mathrm N_{a v}$.
• The mass of one mole of a substance is known as the molar mass. It has units of $\mathrm{g}$ $\mathrm{mol}^{-1}$.
• Avogadro's hypothesis states that the volume $\rm (V)$ of a gas is proportional to the amount $(n)$.
  This can be incorporated into the combined gas equation given earlier to give:
  $\rm P_{1} V_{1} / n_{1} T_{l}=P_{2} V_{2} / n_{2} T_{2}=R$
  $\rm R$ doesn't depend on any of the conditions and is the same for all gases. It is the gas constant.
  This is expressed in the ideal gas equation: $\mathrm{P V} = n \rm R T$.

• Pressure is defined as the normal force per unit area acting on a surface: $\rm P=F \cos \theta / A$
• The unit of pressure is $\mathrm{N} \mathrm{m}^{-2}$ and this is known as the pascal, $\mathrm{Pa}$.
  
• Gases produce force on the walls of a container as the momentum of a gas particle changes from $-m ~v$ to $+m ~v: \Delta p=2~ m ~v$ (in magnitude).
  
• $\Delta p = + p - (-p) = 2~p$
  This change of momentum produces a force according to Newton's Second Law.
  Pressure develops as result of the force from all of molecules colliding with the walls.
• Two molecular properties affect the pressure of a gas:
  • the average speed of the molecules
  • the frequency with which the molecules collide with the walls.

• The ideal gas model explains the ideal gas equation in terms of particle collisions.
• An ideal gas is a theoretical model of a gas:
  • Molecules are hard spheres with negligible radius and volume.
  • All molecular collisions, with other molecules and walls are elastic and are short in duration.
  • Molecules move randomly with a range of speeds.
  • Ideal gases only have random kinetic energy and no intermolecular potential energy in their internal energy.
  • There are no intermolecular forces as the molecules are well separated.
• An ideal gas obeys the equation: PV = nRT at all pressures, volumes, and temperatures
• The gas constant R is universal and has the value $\rm R = 8.31~ J~ mol^{-1}~K^{-1}$.
  $\rm R = PV/nT$. If the conditions are changed from $\rm (P_1, V_1, n_1, T_1)$ to $\rm (P_2, V_2, n_2, T_2)$ : $\rm P_1V_1/n_1T_1 = P_2V_2/n_2T_2$