Non-linear functions, or those whose graphs are not lines, are widely used in modeling and applications. The aim of this chapter will be to examine some nonlinear functions such as quadratic and sinusoidal functions. Whether it is a projectile in motion such as a ball thrown vertically in the air, or weather patterns in a city, many situations follow specific patterns. These patterns are well known and play an important part in the natural sciences and social sciences. One widely used non-linear function is a quadratic function. Quadratic functions model the height of an object after some time has passed after the object is thrown vertically in the air. Specifically:

$h(t) = −4.9t^2 + v_0(t) + h_0$

Where $h(t)$ is the height of the object after $t$ seconds, $v_0$ is the initial velocity of the object in meters per second, and $h_0$ is the initial height the object is released above the ground in meters.

Other popular non-linear models are sinusoidal models. Every function that follows a sinusoidal model can be written as:

$f(x) = a \sin(bx) + d$

Where $a$ is the amplitude, the period is $(360° b)$, and the principal axis is the line $y = d$.

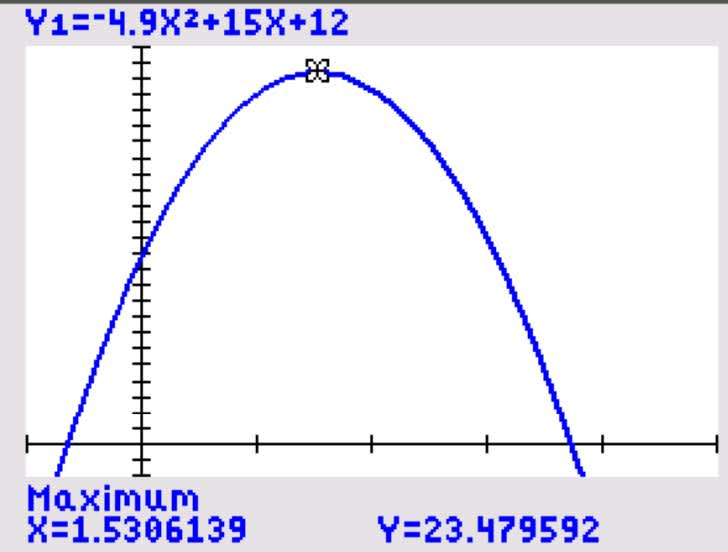
Example: A stone is thrown vertically and its height $h$ after $t$ seconds is given by:

$h(t) = −4.9t^2 + 15t + 12$

Use technology to determine the maximum height the stone reaches.

Explanation: Using the graphing calculator and the 2nd Trace function option 4: maximum gives a maximum height of $23.5$ meters.

Note: This occurs after $1.53$ seconds.