Laws of Sines and Cosines

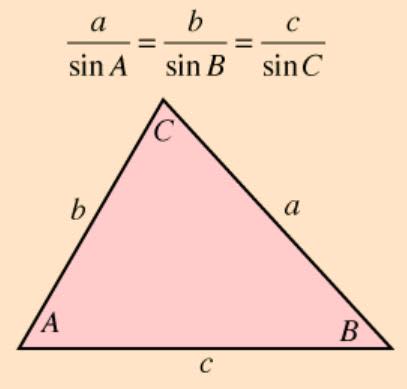
In any triangle, the Law of Sines states that, given angles $\rm A$,$\rm B$ and $\rm C$ with opposite side lengths $a$, $b$ and $c$, then the following ratios are equivalent as seen below:

Example 1: In triangle $\rm ABC$, $m\langle \rm A =32°$, $m\langle \rm B=56°$, and $a=13$. Determine the length of side $b$.

Explanation: Using the Law of Sines gives:

$\dfrac{13}{\sin 32°} = \dfrac{b}{\sin 56°}$
$13\sin 56° = b\sin 32°$
$b = \dfrac{13\sin 56°}{\sin 32°}$ 

Use the TI-84 graphing calculator and make sure the calculator is in degree mode.

Thus, side length $b$ is $20.3$ (to 3 significant figures)

Example 2: In triangle $\rm ABC$, $m\langle\rm A=47°$, $a=6.1$, and $c=5.2$. Determine $m\langle \rm C$.

Explanation: Using the Law of Sines gives:

$\dfrac{6.1}{\sin 47°} = \dfrac{5.2}{\sin \rm C}$
$6.1\sin\rm C=5.2\sin47°$
$\sin\rm C = \dfrac{5.2\sin47°}{6.1}$
$\sin\rm C=0.623$
Thus, $m\langle \rm C=\sin^{−1}(0.623)=38.6°$

Sometimes, using The Law of Sines will not help us. Thankfully, another law has been established. In any triangle, the Law of Cosines states that, given angles $\rm A$, $\rm B$ and $\rm C$ with opposite side lengths $a$, $b$ and $c$, the following equations hold:

$a^2=b^2+c^2−2bc\cos\rm A$
$b^2=a^2+c^2−2ac\cos\rm B$
$c^2=a^2+b^2−2ab\cos\rm C$

Example 3: Consider triangle $\rm ABC$ shown below:

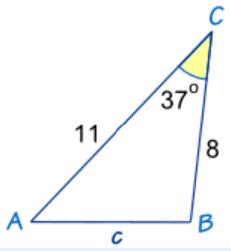
Determine the length of side $c$.

Explanation: Using the Law of Cosines gives:

$c^2=82+112−2(8)(11)\cos37°$
$c^2=64+121−176\cos 37°$
$c^2 =44.44$
$\Rightarrow c=6.67$

It is important to remember that the largest angle in any triangle is opposite the longest side. Likewise, the smallest angle in any triangle is opposite the shortest side. After solving these triangles, it is worth pausing and checking that the largest angle is opposite the longest side and the smallest angle is opposite the shortest side.