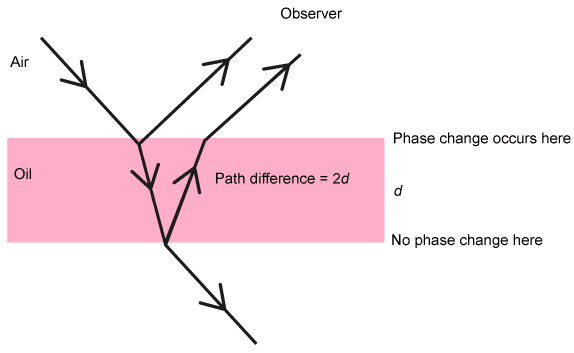
Interference

Interference patterns from multiple slits and thin films produce accurately repeatable patterns.

• For two-source interference to occur the two sources:
  • must be coherent: the phase difference between the sources is constant
  • have approximately the same amplitude
  • have the same polarisation.
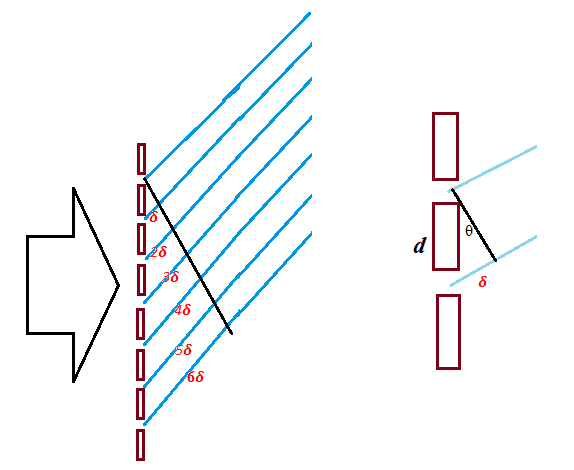
• Bright fringes occur at angles $\theta$ where the path difference corresponds to a whole number of wavelengths. The waves interfere constructively.
  
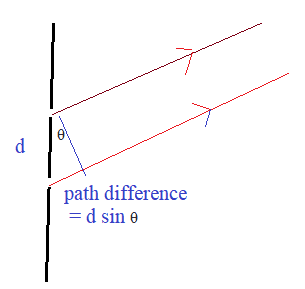
  $d \sin \theta=n \lambda$
  For small angles of $\theta$ in radians $\sin \theta \approx \theta$ when $n=1$
  $d \theta=\lambda$
  Let the distance between the central and first bright fringe $=x$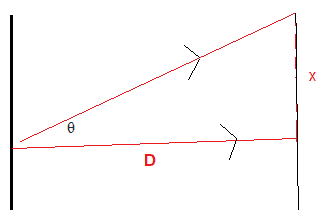
  
  $x=\rm D \theta$
  $x=\mathrm D \lambda / d$
  $\lambda=d x / \mathrm{D}$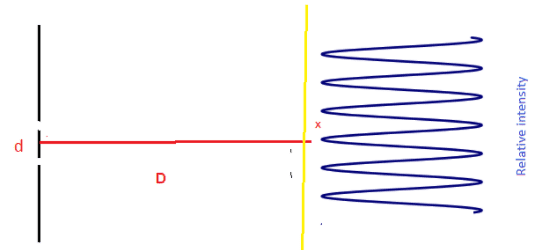
  
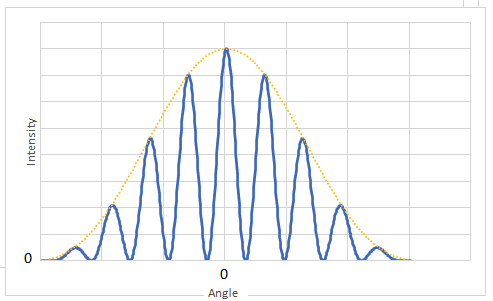
• The diagrams show the intensity observed far from the two slits The pattern shows equally spaced maxima whose intensity is the same.
• The distance between the fringes $x$ increases when the distance $d$ between the slits decreases or when the wavelength increases.

• In practice the diffraction pattern by each slit modifies the double slit interference pattern.
  

• The addition of further slits at the same slit separation has the following effects:
  • the principal maxima maintain the same separation
  • the principal maxima become much sharper
  • the pattern increases in intensity as the overall amount of light admitted increases.

• As the number of slits increases, the interference pattern increases in complexity 
• As the number of slits increases to $\rm N$:
  • the principal maxima maintain the same separation and become thinner and sharper (the width is proportional to $\rm 1/N$)
  • the overall amount of light admitted is increased, so the pattern increases in intensity. The intensity of the central maximum is proportional to $\rm N^2$.
    
• When the path difference between rays from neighbouring slits is $\lambda$ constructive interference occurs between all the rays.
  
  $d \sin \theta=\lambda$
• More generally other maxima occur when the path difference $=n \lambda$
  $n \lambda=\mathrm{d} \sin \theta$

• When a ray of light reflects off a surface that has a higher index of refraction than the medium from which the ray is incident, a phase change of $\pi$ takes place.
  
• The ray in air reflects from the top surface of oil. As the refractive index of oil is greater than that of air a phase change takes place. The second reflection at the bottom surface of oil does not result in a phase change. The two reflected rays interfere. At normal incidence, the path difference is $2d$ where $d$ is the thickness of the film. Assuming a small angle of incidence:
  • Destructive interference occurs if $2 d=m \lambda_{\text {oil }}$ ($\mathrm{m}$ is an integer)
  • Constructive interference occurs if $2 d=(m+½) \lambda_{\text {oil }}$
    $\lambda_{\text {oil }}$ is the wavelength of light in the oil and $m=0,1,2,3$ etc.
    From Topic 4 $v_{\text{air}} / v_{\text {oil}}=n_{\text{oil}} / n_{\text{air}}$ $=\lambda_{\text{air}} / \lambda_{\text {oil }}$
    $\lambda_{\text {oil }}=\lambda_{\text {air }} / n_{\text {oil }}$
  • So for destructive interference occurs if $2 d=m \lambda_{\text {oil }}=m \lambda_{\text {air }} / n_{\text {oil }}$
  • And constructive interference occurs if $2 d=(m+½) \lambda_{\text {oil }}$ $=(m+½) \lambda_{\text {air }} / n_{\text {oil }}$
• A layer of oil floating in water will show a coloured oil film. The colour at a particular angle θ seen is determined by:
  • white minus that colour whose wavelength that destructively interferes at $\theta$
  • the colour that constructively interferes at θ
• As the oil film has variable thickness different colours are observed at different parts of the film.
• Thin-film interference occurs in high-quality lenses where a thin coating is added on the lens. This causes destructive interference at certain wavelengths, and so reduces the reflected light.