Forces

A force is needed to change a state of motion, as suggested by Newton in his laws of motion.

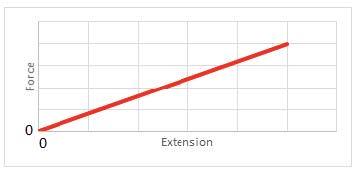
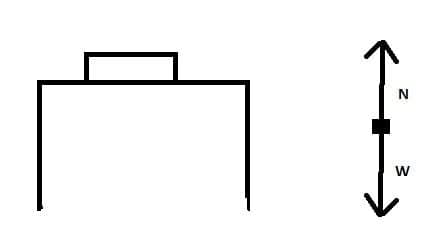
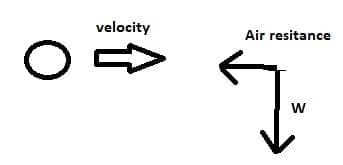
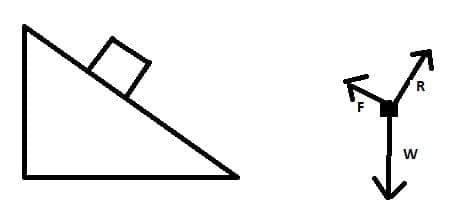
• Forces are vectors and are represented by arrows whose length is a measure of the magnitude of the force. The direction of the arrow gives the direction of the force.
• The Net (resultant) force is the combined vector sum of all the individual forces on the body.
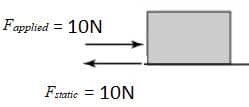
• When the net force on a body is zero the body remains at rest or moves with constant velocity.
• If the resultant force on a body is zero then the forces are said to be in equilibrium.
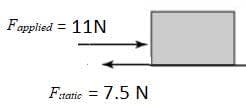
• Unbalanced force causes acceleration of the body on which the force acts.
  If a body accelerates then the forces on it are unbalanced.

• The simplest experimental method for measuring the size of a force is to use the extension of a spring.
• Hooke’s law states that up to the elastic limit, the extension, $x$, of a spring is proportional to the tension force, $\mathrm F = k~x$
  $k$ is the spring constant with units of $\rm N~ m^{-1}$.

• A free body diagram shows the forces on one body which is shown as a point. All the forces are shown and labelled.

A free body diagram of a book on a table.	A free body diagram of a ball moving in the air. Note there is no force acting in the direction of the velocity.
A box stationary on a slope.	An object accelerating upward in an elevator.

• For a constant mass the net force on a body of constant mass is = mass the acceleration of the mass:
  $\bf F_{net} = ma$.
• The $\rm SI$ unit of force is the newton. $\rm F = 1~N$ when $\rm m = 1~kg$ and $\rm a = 1~m~s^{-2}$.
• A more general expressions of the law: the rate of change of momentum is equal to the net force and takes place in the same direction.
  $\mathrm F = \Delta p/\Delta t$

• If a body $\rm A$ exerts a force on body $\rm B$, then $\rm B$ will exert an equal and opposite force on $\rm A$. For example:
  • A rocket for example exerts a force on the exhaust gases pushing them backward and the gases exert an equal and opposite force on the rocket pushing it forward.
  • A helicopter rotor exerts a force on air pushing air downwards. The air exerts an equal, upward force on the rotor.
• Newton's third law also applies where there is no contact between the bodies. For example:
  • the electric force between two electrically charged particles
  • the gravitational force between any two massive particles.
    These forces must be equal and opposite.
• The two forces in the pair act on different objects – this means that equal and opposite forces that act on the same object are NOT Newton’s third law pairs.
  The two forces in the pair they must be of the same type: if the force that A exerts on B is gravitational force, then the equal and opposite force exerted by B on A is also a gravitational force.

• Friction is the force that opposes the relative motion of two surfaces. It arises because the surfaces involved are not perfectly smooth on the microscopic scale.
• Static friction acts when there is no relative motion between the surfaces.
• The static friction force changes with the applied force up to a certain maximum force, $\bf F_{\max }$
  $\rm F_{\text {applied }}=F_{\text {static }}$ when $\rm F_{applied} \leq F_{\max}$
• $\rm F_{\max }$ depends upon:
  • the nature of the two surfaces in contact.
  • the normal reaction force (R) between the two surfaces. $\rm F_{\max }=\mu_{\text {Startic }} \mathrm{R}$
    $0 \leq \mu_{\text {static }} \leq 1$
• Dynamic friction acts when there is relative motion between the surfaces. The dynamic frictional force is less than the maximum static friction force.
  $\rm F_{\max }>F_{dyn}$
  The dynamic frictional force can be considered as approximately independent of the speed.
• As the maximum value for dynamic friction is less than the maximum value for static friction, $\mu_{\text {static }}>\mu_{\text {dyn}}$

Consider the example with a mass of $5 \mathrm{~kg}, \mu \mathrm{s}=0.2$ and $\mu_{\mathrm{d}}=0.15$
$\mathrm{~W}=\mathrm{mg}=50 \mathrm{~N}$ and $\mathrm{R}=\mathrm{W}=50 \mathrm{~N}$
$F_{\max }=\mu \mathrm{s} \mathrm{R}=0.2 \times 50=10 \mathrm{~N}$
$F_{dyn}=7.5 \mathrm{~N}$

	Object is static
	Object is static
	Object is static but $\rm F_{static} = F_{max}$
	$\rm F_{\text {applied }} \geq F_{\max}$ The object is moving and so the dynamic friction acts. Friction is reduced: $\rm F_{dyn}=7.5 \mathrm{~N}$ $\rm F_{net}=11-7.5=3.5 \mathrm{~N}$ $\rm a=F / m=3.5 / 5=0.70 \mathrm{~ms}^{-2}$