Similar approaches can be taken when analyzing electrical and gravitational potential problems.
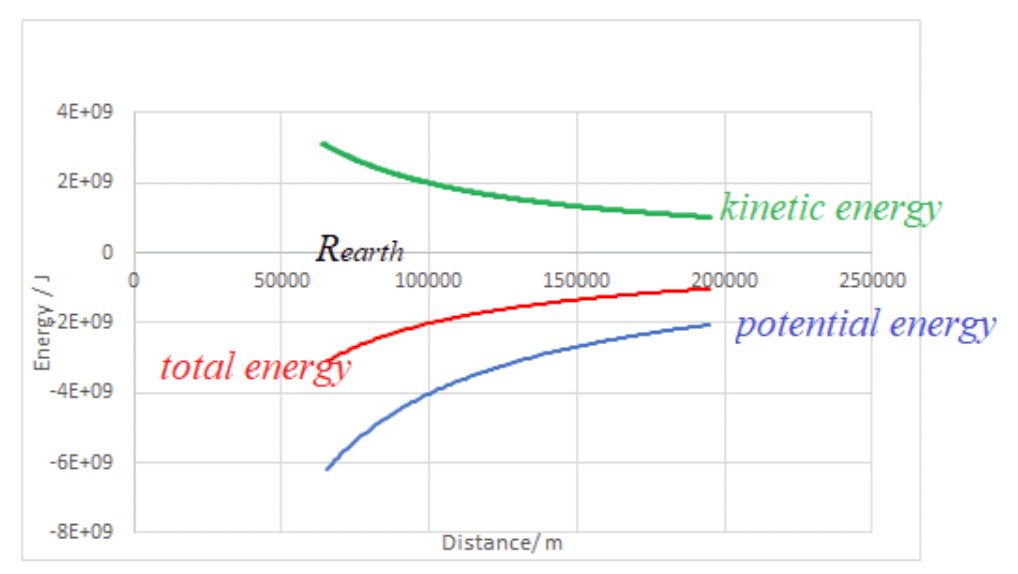
Gravitational potential energy
- The work done in moving a point mass m from infinity to a point near a mass $\rm M$ is:
$\rm W = −GMm/\cal r$ - The gravitational potential energy between the two masses decreases as they are moved together:
$\rm E_P=-GMm/\cal r$ - The gravitational potential energy is always negative relative to a body at infinity as the force is attractive.
- The gravitational potential energy of a mass m placed at point where the gravitational potential is $\rm V$ is:
$\rm E_p = mV$
Electric potential energy
- The work done in moving a positive point charge q from infinity to a point near a charge $\rm Q$ is:
$mathrm W = k\mathrm Qq/r$ - This work increases the electric potential energy between the two charges:
$E_P=kQq/r$ - The electric potential energy is negative relative to infinity if $\rm Q$ is negative, and the force is attractive. It is positive if $\rm Q$ is positive and the force is repulsive
- The electric potential energy of a charge $q$ placed at point where the electric potential is $\rm V$ is $\mathrm E_p=q\rm V$
The relation between field and potential
- Consider the movement of a body in a gravitational field $(g)$:
The work done in moving a mass $\rm (m)$ from $\rm A$ to $\rm B = m\Delta V_g{^{BA}} = -m\Delta V_g{^{AB}} = \mathrm F\Delta x$
$\mathrm F\Delta x = \rm \Delta V_g{^{AB}}$
$\rm F/m = \rm\Delta V_g{^{AB}}/\Delta \cal x$
$g = -\rm \Delta V_g{^{AB}}/\Delta \cal x$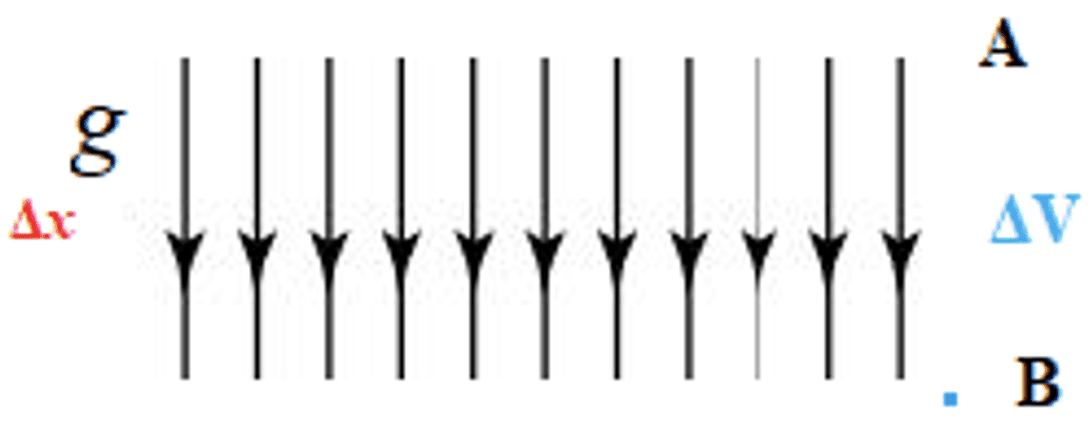
 Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA