Many exponential equations can be solved by rewriting each base number as one or the other. Unfortunately, many other exponential equations cannot be solved this way and require the use of other techniques. These other techniques include the use of logarithms. To understand this, let’s look at a few examples of exponential equations that can be solved without the use of logarithms. However, first recall the rules for exponents:
- $x^a\cdot x^b = x^{a-+b}$
- $\dfrac{x^a}{x^b} = x^{a-b}$
- $(x^a)^b = x^{ab}$
- $x^{-a} = \dfrac{1}{x_a}$
Example 1: $\left(\dfrac{1}{2}\right)^{2𝑥+1} = 4^{𝑥−1}$
Notice the base numbers are $\dfrac{1}{2}=2^{−1}$ and $4$. Since this is the case, rewriting both sides of the exponential equation with a base 2 yields:
$\left(\dfrac{1}{2}\right)^{2x+1}= 4^{x−1}$
$(2^{−1})^{2x+1} = (2^2)^{x−1}$
$2^{−2x−1} = 2^{2x−2}$
Since both bases are equal, this implies that the exponents must be equal. Therefore:
$−2x−1=2x−2$
$−4x=−1$
$x=\dfrac{1}{4}=0.25$
Oftentimes, it is not possible to write both numbers as the same base like we did in the previous example. This is where logarithms play a role. The exponential equivalent of an equation in logarithmic form is:
If $x^a = b$, then $\log_xb=a$
There are $3$ rules for logarithms which follow from the first three rules of exponents stated at the start of the chapter. Without going into a formal proof, they are:
- $\log_x(ab)=\log_xa+\log_xb$
- $\log_x\dfrac{a}{b} = \log_x a−log_xb$
- $\log_xa^b = b \log_xa$
Example 2: Solve the exponential equation $3 = 2^{x−1}$
Notice that the base numbers are $3$ and $2$ and it will not be possible to rewrite both base numbers as a $2$ or a $3$. Thus, logarithms are required. Rewriting this exponential equation as a logarithmic equation gives:
$3 = 2^{x−1}$
$\log_2 3 = x − 1$
$\log_2 3 + 1 = x$
Note that $\log_2 3$ is the number that $2$ must be raised to in order to obtain $3$. Once this is determined, add 1 and that is the solution. Using the TI-84 CE graphing calculator gives:
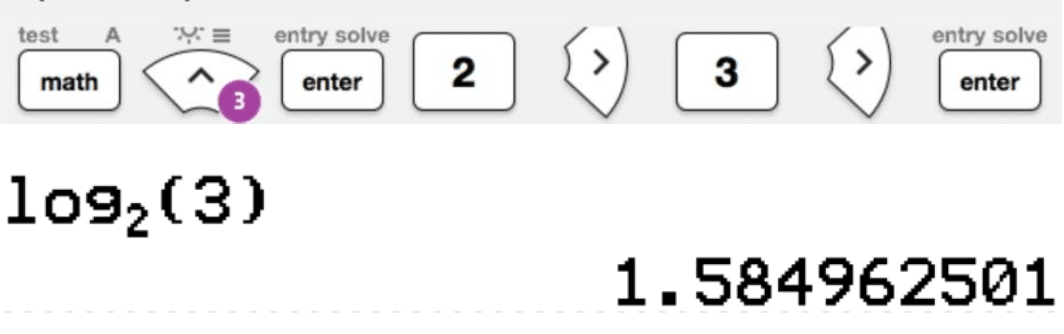
Thus, to $3$ significant figures, $x = 1.58 + 1 = 2.58$
 Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
