The concept of the energy change in a single step reaction being equivalent to the summation of smaller steps can be applied to changes involving ionic compounds.
- Energy cycles allow for the calculation of values corresponding to certain enthalpy changes which cannot be determined directly.
- The standard state of an element or compound is its most stable state under the standard conditions (pressure $\rm 100 kPa$, temperature $\rm 298~K$).
- The enthalpy of formation of any element in its stable state is zero as there is no enthalpy change when an element is formed from itself.
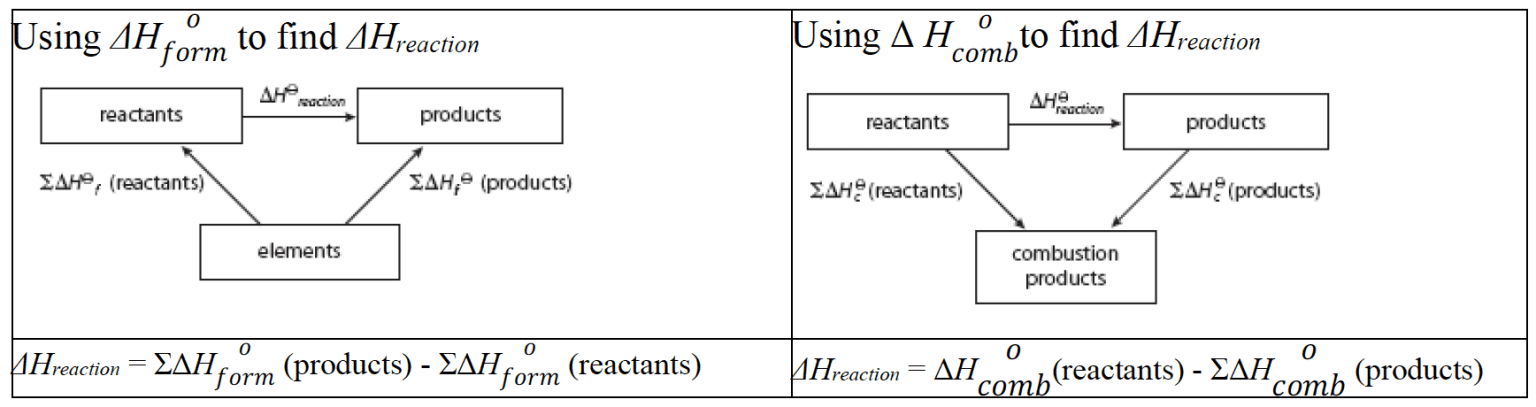
- $\rm\Delta H_{reaction}$ calculated from $\rm\Delta H^o_{form}$ or $\rm\Delta H^o_{comb}$ is more accurate than $\rm\Delta H_{reaction}$ values based on bond enthalpies which apply only to the gaseous state and are average values.
- The first electron affinity is the enthalpy change when one mole of gaseous atoms attracts one mole of electrons: $\rm X(g) + e^-(g) \rightarrow X^-(g) \qquad \Delta H^o_e$
- The lattice enthalpy is the enthalpy change that occurs when one mole of a solid ionic compound is separated into gaseous ions under standard conditions. For example, for alkali metal halides:
$\rm MX(s) \rightarrow M+(g) + X^-(g) \qquad \Delta H^o_{lattice}$ - $\rm \Delta H^o_{lattice}$ depends on the attraction between the ions:
- an increase in the ionic radius of the ions decreases $\rm\Delta H^o_{lattice}$.
- an increase in ionic charge increases $\rm\Delta H^o_{lattice}$.
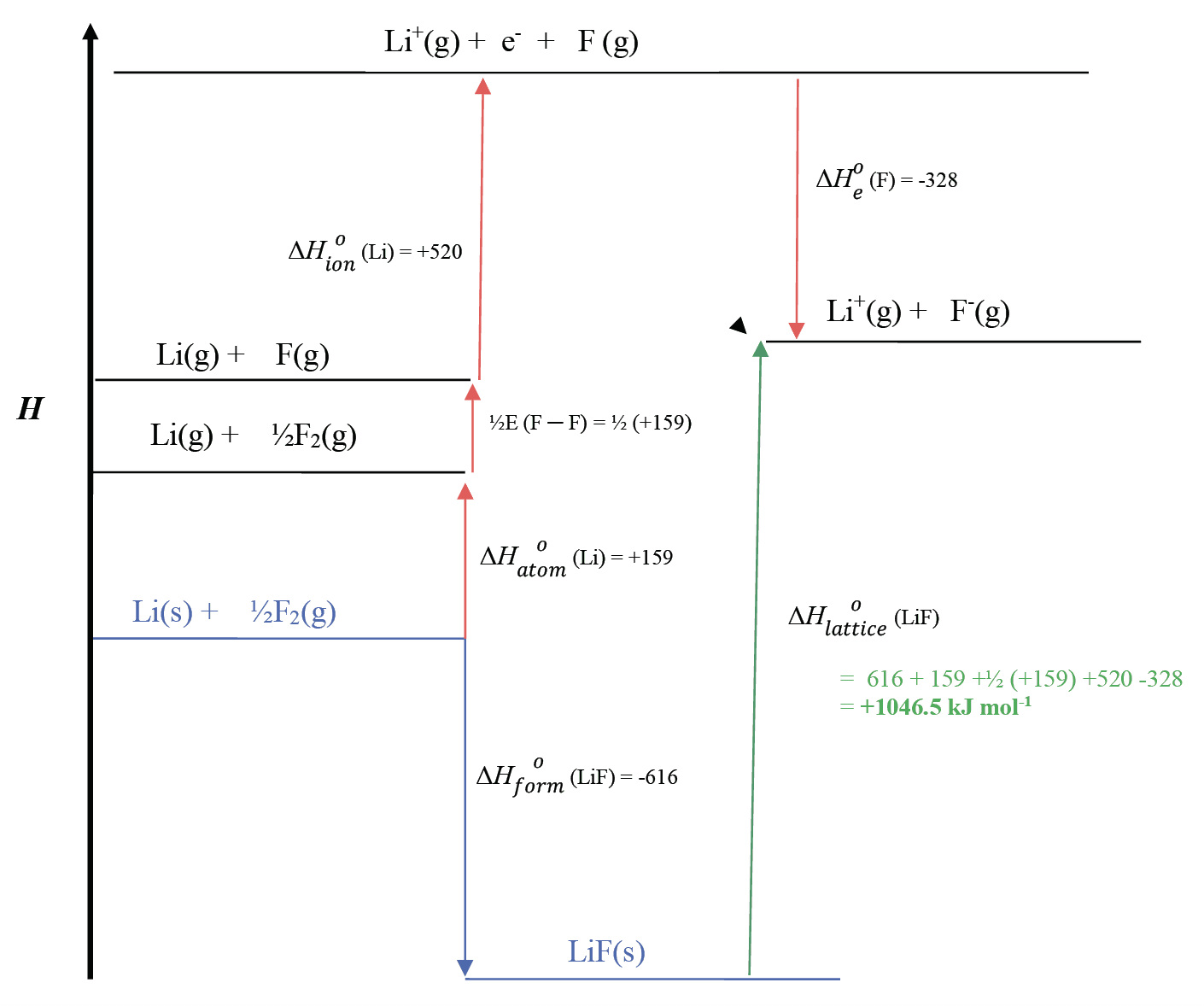
- The Born-Haber cycle, a special case of Hess’s law for the formation of ionic compounds. It allows the lattice enthalpy to be calculated from other enthalpy changes.
- Lattice enthalpy values from Born-Haber cycle are experimental values, as they are based on other experimental data.
- Theoretical lattice enthalpies can be calculated using a (purely) ionic model from the ionic charges and radii.
- Differences between the theoretical and experimental lattice enthalpies give an indication of the covalent character of the compound: the greater the difference the more covalent the compound.
Born Haber Cycle for LiF
- The hydration enthalpy is the enthalpy change that occurs when one mole of gaseous ions are converted into aqueous ions under standard conditions. For example, for alkali metal halides:
$\rm M^+ (g) \rightarrow M^+(aq) + \Delta H^o_{hydration} (M^+)$
$\rm X^-(g) \rightarrow X^-_{(aq)} + \Delta H^o_{hydration} (X^-)$ - All hydration enthalpies are exothermic as they involve an increases in interaction between ions and polar water molecules.
- The hydration enthalpy of an ion depends on the attraction between the ion and the polar water molecules.
Worked Example
Determine the hydration enthalpy of the $\rm Li^+$ ion from the enthalpy cycle and data given.
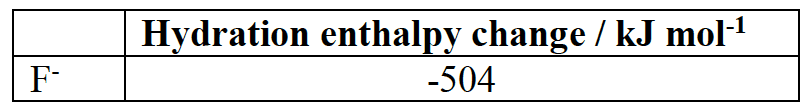
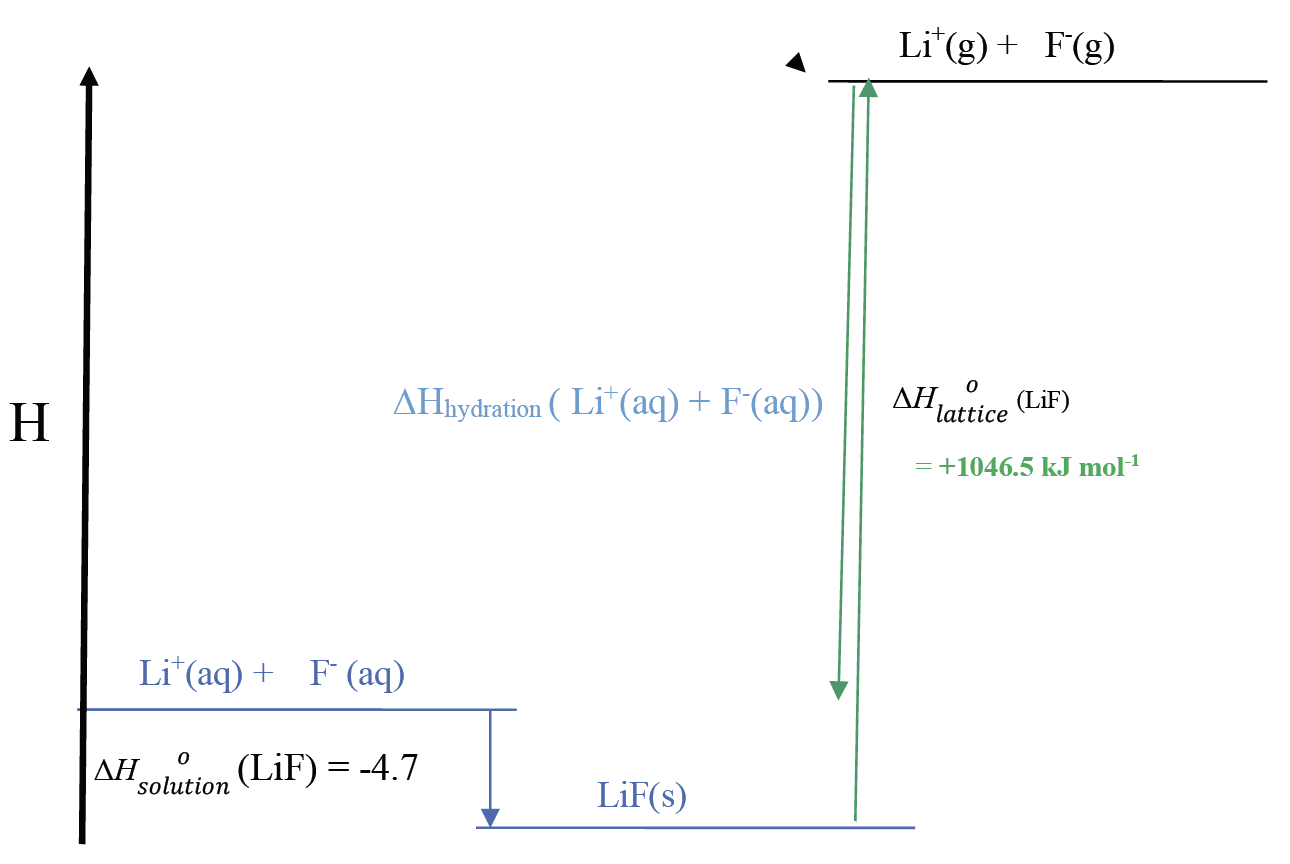
Solution
$\rm \Delta H_{hydration} (Li^+ + F^-)$ $= -1046.5 + 4.7$ $= -1041.8$
$\rm\Delta H_{hydration} ( Li^+ + F^-)$ $\rm = -504 + \Delta H_{hydration} ( Li^+)$
$\rm -1041.8 = -504 + \Delta H_{hydration} (Li^+)$
$\rm \Delta H_{hydration} (Li^+)$ $= -1046.5 + 504$ $\rm = -542.5~kJ~mol^{-1}$
 Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
