Electron configuration

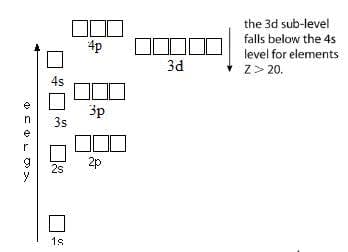
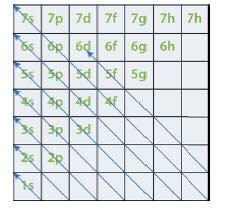
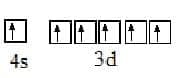
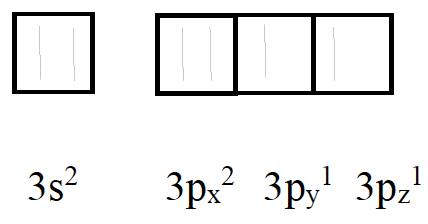The electron configuration of an atom can be deduced from its atomic number

• The electromagnetic spectrum includes in order of increasing frequency/energy:
  radio waves, microwaves, IR radiation, visible light, ultraviolet radiation $\rm X-$rays, and $\gamma$ rays. (See section $3$ of the IB data booklet)
• The frequency $(v)$ and wavelength $[\lambda]$ are related by: $\rm c$ (speed of light] $= \lambda v$.
• The energy of a photon of light $\rm E_{photon}$ is related to the frequency $[v]$ of the radiation by Planck's equation:
  $\mathrm{E_{photon}} = h\nu = \dfrac{hc}{\gamma}$, (the equation is given in section $1$ of the IB data booklet)
  $\rm h$ is Planck's constant $\rm 6.63 \times 10^{-34}~Js.h$ is Planck’s and $\rm c$ is the speed of light $\rm = 3.00 \times 10^8~m~s^{-1}$ (see section $2$ of the IB data booklet}.
• A continuous spectrum contains radiation of all wavelengths within a given range ($\rm e.g.$ the visible spectrum).
• A line spectrum consists of discrete lines of different wavelengths / frequencies. An emission spectrum of hydrogen atom consists of different series of lines against a dark background in different regions of the electromagnetic spectrum. An absorption spectrum is like a “negative” of a emission spectrum and consists of a series of dark lines against a coloured background.
• The emission spectrum of hydrogen atom consists of different series of lines in different regions of the electromagnetic spectrum. The lines are produced when excited electrons fall from higher to lower energy levels.
  

  Energy levels of hydrogen atom	Lines in the emission spectra (Lyman series)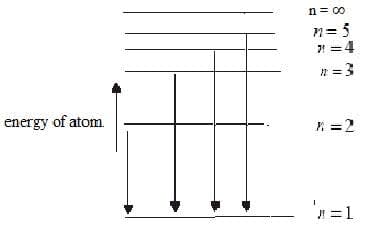

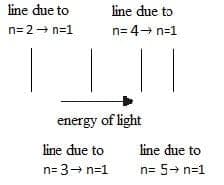
• Each photon of light is emitted when an electron falls from an excited state to a lower energy level and corresponds to a particular energy wavelength and frequency. $\mathrm{E_{photon}} = h\nu = \dfrac{hc}{\gamma}$.
• Transitions where the electron falls to the $\rm n = 1$ give out the most energy and are in the ultraviolet region. Transitions to $\rm n = 2$ are of less energy and are in the visible region and transitions to $\rm n = 3$ are in the infrared region.     
• The line emission spectrum of hydrogen provides evidence for electrons occupying discrete energy levels.
• The energy levels of the hydrogen atom converge at higher energy as they are further from the nucleus, and the lines in the spectrum also converge at higher energy/frequency.
• The limit of convergence $\rm n = \infty$ corresponds the electron leaving the atom. The energy between the $\rm n = 1$ and $\rm n = \infty$ energy levels is called the ionisation energy.

The Aufbau Principle

• The Bohr model of the atom had a number of limitations and was superseded by a model in which each electron occupy atomic orbitals.
• An atomic orbital is a region of space where there is a high probability of finding an electron Each orbital can hold two electrons of opposite spin. (The Pauli exclusion principle)
• There are different types of orbital with characteristic shapes. s orbitals are spherical, p orbitals, which orientated along the x, y and z are dumb–bell shaped.
  

  An s orbital which can hold a maximum number of 2 electrons of opposite spin.	A $\rm p\gamma$ orbital which can hold a maximum number of $2$ electrons of opposite spin. There are similar $\rm p$ orbitals of the same energy orientated along the $\rm x$ and $\rm z$ axis.
  	The three $\rm p$ orbitals all have the same energy and from a $\rm p$ sub-level.

• You are not required to know the shape of d and $\rm f$ orbitals which are more complex. The five orbitals form a d sub-level and the seven $\rm f$ orbitals from a $\rm f$ sub-level.
• The relationship between sublevels and atomic orbitals is as follows:
   
• The main energy levels of electrons in atoms {in order of increasing energy) are identified by integers, $\rm n=1,2,3,4,$…
• Each main energy level contains n sublevels and $\rm n^2$ orbitals.
• For example there are $3$ sublevel $\rm (3s, 3p~ and ~3d)$ and $9$ orbitals in the third energy level and $\rm 3d$ and only $2$ sublevels $\rm(2s$ and $\rm 2p)$  and four orbitals in second energy level $\rm(2s$ and $\rm2p)$.
  
• The electron configuration of an atom describes the number of electrons in each energy sub-level and can be deduced from its atomic number.

Deducing the Electron configuration of atoms

There is a useful mnemonic to the order of filling orbitals. Follow the arrows to see the order in which the sublevels are filled: $\rm 1s < 2s < 2p <$, $\rm 3s < 3p< 4s$ $\rm < 3d <4p < 5s$, $\rm 4f < 5d < 6p < 7s$

•  The Aufbau principle states that orbitals with lower energy are filled before those with higher energy.
• Hund's rule states that every orbital in a sublevel is singly occupied with electrons of the same spin before any one orbital is doubly occupied.
  Worked Example
  Deduce the electron configuration of sulfur.
  Solution
  Sulfur has an atomic number of $16$. It has $16$ electrons.
  Two electrons occupy the $\rm 1s: 1s^2$
  Two electrons occupy the $\rm 2s: 2s^2$
  Six electrons occupy the $\rm 2p: 2p^6$
  Two electrons occupy the $\rm3s: 3s^2$
  Four electrons occupy the $\rm3p: 3p^4$
  Answer $\rm 1s^2$ $\rm 2s^2$ $\rm 2p^6$ $\rm 3s^2$ $\rm 3p^4$ 

• Sometimes it is appropriate to use a condensed electron configurations where square brackets represent the electron configuration of the previous noble gas core. So for sulfur this would be: $\rm [Ne]3s^2$ $\rm 3p^4$ (as $\rm Ne$ has the electron configuration $\rm 1s^2~2s^2~2p^6$)
• To show how the electrons are arranged within a sublevel we need to Hund's rule. So sulfur has two $\rm 3p$ orbitals with one electron and the third $\rm 3p$ orbital with two.
  $\rm e.g. S: [Ne]$
            
• The $\rm 4s$ and $\rm 3d$ orbitals are very close in energy and their relative energies changes with atomic number as outlined above This explains the unusual electron configurations of chromium and copper. Chromium has an atomic number of $24$. The six electrons in the $\rm 4s$ and $\rm 3d$ orbitals do not have the configuration expected from the Aufbau principle and instead adopt a configuration in line with Hund’s rule if the $\rm 4s$ and $\rm 3d$ had the same energy. All the six orbitals are singly occupied.
  
  Copper is also unusual with the electron configuration if $\rm 3d^{10}$ and $\rm 4s^1$. The stability of these configurations can be explained in terms of the stability of the half- full ($\rm 3d^5$ and full $\rm(d^{10})d$ sub-shell.
• The block nature of the Periodic Table is determined by the highest energy occupied sub-level. Elements in the $\rm s$ block have outer valence electrons in $\rm s$ orbitals; elements in the $\rm p$ block have valence electrons in the $\rm p$ sublevel.
  

Deducing the Electron configuration of ions

• A positive ion is formed when electrons are removed from a neutral atom. The electron configuration of $\rm Na$ is $\rm 1s^2s2p^63s^1$ and $\rm Na^+$ is $\rm 1s^2s^2p^6$. The electrons are always removed from energy levels with the highest value of  $\rm n$. For example, $\rm Mn$: $\rm [Ar]3d^54s^2$, but $\rm Mn^{2+}$: $\rm [Ar]3d^5$
• Negative ions are formed by adding electrons to a neutral atom. The electron configuration of $\rm F$ is $\rm 1s^2s^2p^5$ and $\rm F^-$ is $\rm 1s^22s^2p^6$.