Electromagnetic induction

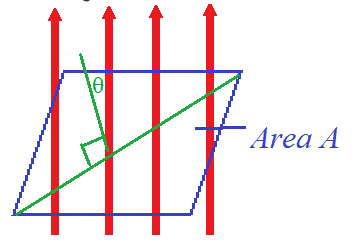
Electricity is mostly generated by machines using electromagnetic induction.

• Consider a rod of length $\rm L$ that is moved with velocity $v$ in a magnetic field $\rm B$, going into the plane of the page.
  
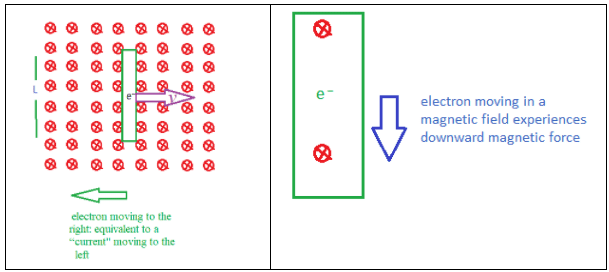
• As the rod moves its many ‘free’ electrons also move from left to right. The movement of electrons is equivalent to an “electric current” and the electrons experience a downward magnetic force.
• As the electrons move downward through the wire, the bottom end builds up a negative charge and the top end a positive charge. The movement of electrons towards the bottom becomes more difficult as the charge difference builds up and eventually stops.
  
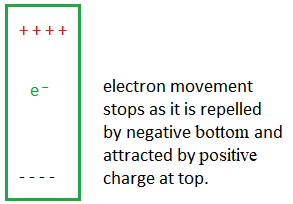
• The charge difference produces an electric field $\rm (E)$, and a potential difference known as the induced electromotive force, $\rm emf(\varepsilon)$.
  From topic 10: $\rm E=-\Delta V / L=-\varepsilon / L$
• The flow of electrons stops when the electric force $\rm e E$ pushing the electrons up equals the downward magnetic force $\rm e \mathcal v B$.
  $\rm e E=B e \mathcal v$
  $\rm e \varepsilon / L=B e \mathcal v$
  $\rm \varepsilon=B \mathcal v L$
• The moving rod can behave as a battery when connected to a resistor in a complete circuit and produces an induced current (I).
  $\rm \varepsilon=B \mathcal v L=I R$
  $\rm I=B \mathcal v L / R$
• As the induced current is in a magnetic field it in turn experiences a magnetic force: $\rm F=B I L$ and the rod needs to be pushed if it is to continue to move at constant speed $v$:
  $\rm F=B \mathcal I L=B(B \mathcal v L / R) L=\mathcal v B^{2} L^{2} / \mathrm{R}$
• This force generates power $\rm (P)$ : $\rm P=F \mathcal v = \mathcal v^{2} B^{2} L^{2} / R$
• The power is dissipated in the circuit as heat in the resistor:
  $\rm P=\varepsilon^{2} / R=\mathcal v^{2} B^{2} L / R$
  In this process mechanical work is transformed into electrical energy and then heat. $\rm \varepsilon^{2}=\mathcal v^{2} B^{2} L$ and $\rm \varepsilon=B  \mathcal{lv}$ as expected.

• Magnetic flux $(\Phi)$ goes through a loop of wire when it is placed in a magnetic field.
• If a loop of area $\rm A$ is placed in a region of uniform magnetic field $\rm B$ at an angle $\theta$ between the direction of the magnetic field and the normal the magnetic flux $(\Phi)$ through the area is: $\rm \Phi=B A \cos \theta$
  
  The flux is a maximum when the field is perpendicular to the area $\rm A$ and $0$ when the field is parallel to the area. 
  

  If the field is parallel to the area there is no flux through the wire.	If the field is normal to the loop the flux is a maximum. $\rm \Phi=N B A$

• If the wire has $\rm N$ loops the magnetic flux linkage $(\Phi)$ through the loop is: $\rm \Phi=N B A \cos \theta$

• As the wire moves through a magnetic field shown we have $\rm \varepsilon=B \mathcal v L$
  
  The wire covers an area $\rm \Delta A$ of the magnetic field in $\Delta t$ :
  $\Delta \mathrm{A=L} v \Delta t$
  $L v=\Delta \mathrm{A} / \Delta t$
  $\rm \varepsilon=B \Delta A / \Delta \mathcal t$
• As the field is at right angles to the area $\rm B \Delta A$ is the change in magnetic flux $(\Delta \Phi)$. $\varepsilon=\Delta \Phi / \Delta t$
• Faraday's law of induction states that the induced emf $(\varepsilon)$ in a loop is equal to the rate of change of magnetic flux linkage with time:
  $\varepsilon=-\Delta \Phi / \Delta t$
  The negative sign arises from Lenz's law.

• Lenz’s law’s states that the direction of the induced emf opposes the change in flux that created it:
  • if the flux is increasing the induced current must produce a magnetic field opposite to the external field
  • if the flux is decreasing the induced current must produce a magnetic field parallel to the external field.
• Lenz’s law is an application of the law of conservation of energy: if the direction of an induced current did not oppose the change that caused it, it would support the change and a force would be generated that further accelerated the moving object. This would generate an even larger emf and electrical energy would be generated without work being done.