Electric fields

📝 Mini-cours GRATUIT

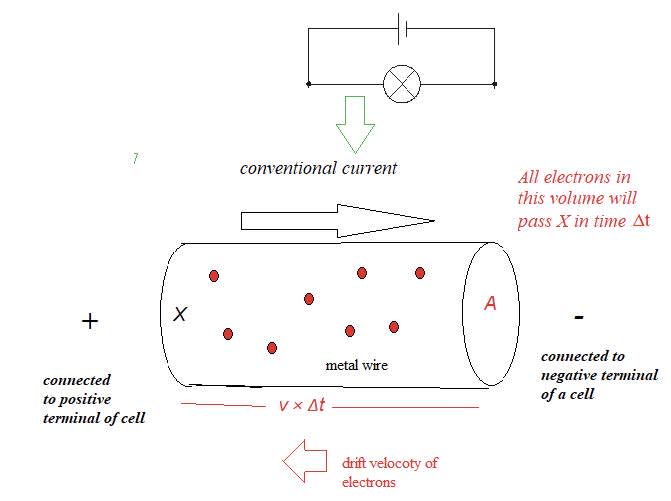
When charges move an electric current is created.

Two types of charge exist – positive and negative.
Charge is always conserved. The total charge before any process equals the total charge afterwards. Objects can be charged by friction when electrons are physically moved from one object to another.
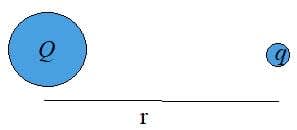
Two point charges $q_{1}, q_{2}$ separated by a distance $r$ exert a force on each other: $\mathrm F=k q_{1} q_{2} / \rm r^{2}$
The Coulomb constant $(k)=8.99 \times 10^{9} \mathrm{~N.m}^{2} \mathrm{C}^{-2}$.
$k=1 / 4 \pi \varepsilon_{0}(\varepsilon_{0}$ is the permittivity of free space $=8.85 \times 10^{-12} \mathrm{C}^{2} \mathrm{~N}^{-1} \mathrm{~m}^{-2})$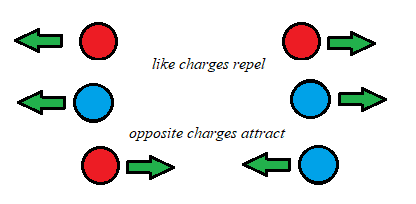
If there are two or more charges near another charge, the overall force can be worked out using vector addition.

Charge cannot move through an insulator as there are very few free electrons.
Plastics, wood and glass are examples of electrical insulators.
Charge can move through a conductor as there are free electrons. All metals and graphite are conductors.

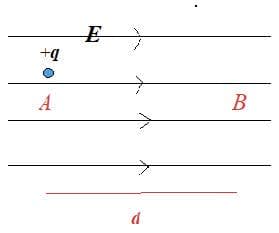
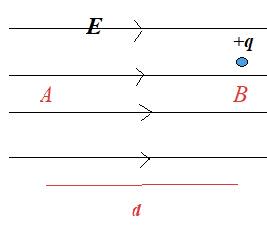
An electric charge $Q$ creates an electric field in the space around it. This fields acts on other charges by exerting an electric force.
The Electric field $\rm (E)$ at a point is the electric force per unit charge exerted on a small, positive point charge $q$ placed at that point. It is a vector quantity.
For a charge $Q$.
$\mathrm{E}=F / q =k Q q / \mathrm{qr}^{2}$
$\mathrm{E}=F / q =k Q / \mathrm{r}^{2}$

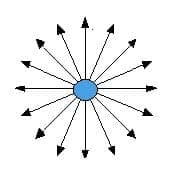
The electric field of a positive charge.

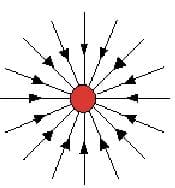
The electric field of a negative charge.


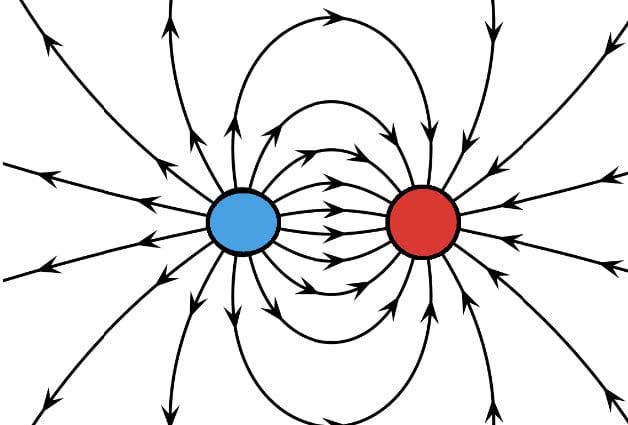
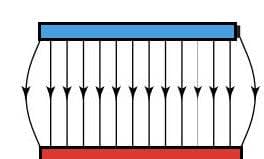
The electric field of a positive and negative charge.	The electric field due to parallel positive and negative plates.

Electric field lines:
- begin on positive charges and end on negative charges
- never cross
- are close together when the field is stronger.

The electric potential $\bf (V)$ is the work done per unit charge in moving a (positive) point charge $q$ from infinity to a point near the charge $Q$ is $\mathrm{V = W}q$
The unit of electric potential is the volt $\rm (V)$ and is equivalent to $\rm J.C^{−1}$.
The work done is independent of the path followed.
The electric potential a distance $r$ from a particle of charge $Q$:
$\mathrm V = kQ/r$

The work done in moving a positive point charge $q$ from infinity to a point near a charge $Q$ is:
$\mathrm W = Q\mathrm V= kQq/r$
This energy is stored as electric potential energy between the two charges:
$\mathrm{Ep}= kQq/r$
In general, the electric potential energy of a charge $q$ placed at point where the electric potential $\rm V$ is:
$\mathrm{Ep} = q\rm V$
The potential difference $\rm (V)$ is the work done per unit charge in moving charge between two points:
$\Delta\mathrm{V = W}/q$

An electric charge in an electric field experiences a force. If the charge moves due to the electric field, work is done on the charge. The charge loses potential energy and gains kinetic energy.

Work done on charge from $\rm A$ to $\rm B = force \times distance$ $= \mathrm{Eq} \times d = \text{kinetic energy gained}$ $\rm = ½ ~mv^2$
$\mathrm{Eq} \times d = \rm ½ ~mv^2$
If the charge moves against the field, the work is done on the charge against the field and the potential energy increases.

$\rm Eqd = \text{increase in potential energy}$ $= q\Delta \rm V_{AB}$
$\rm E = \Delta V_{AB}/\mathcal d$

Electric Currents

An electric field occurs as a result of a potential difference $\rm (E = \Delta V/ \mathcal d)$. An electric cell or battery can be used to set up a potential difference in a circuit.
When an electric field is set up within a conductor, any free electrons experience a force in a direction opposite to the electric field as they have a negative charge.
These electrons have net motion in the opposite direction to the electric field. This is net motion is an electric current. The magnitude of the electric current is the amount charge that passes a point in a circuit per unit time.
$\rm I = \Delta Q/ \Delta \mathcal t$
The unit of current is the ampere, $\rm 1 ~A = 1~C.s^{−1}$.
In $\rm SI$ units, the ampere is the base unit and the coulomb is a derived unit
By convention the direction of the current is the direction that a positive charge would move in the circuit. This is same as that of the electric field, from the positive to the negative terminal of a cell.
The current is the same at all points in a series circuit.
The current is related to the electron drift velocity.

$n =$ number of the charge-carriers per unit volume that are available to move
$q = \rm charge$ $v = \text{average speed}$
number of charge-carriers that pass $\rm X$ in interval $(\Delta t)= n \times \mathrm Av\Delta t$
charge that passes $\rm X$, $\Delta \mathrm Q = n\mathrm Av\Delta t \times q$
current $\mathrm I =\Delta \mathrm Q/\Delta t = n\mathrm Avq$