Electric cells

Electric cells allow us to store energy in a chemical form.

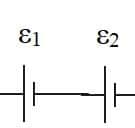
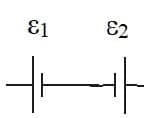
• In a battery chemical energy is converted into electrical energy. The emf is the joules of electrical energy given to each unit of charge.
• So far we have assumed that the internal resistance of the battery or power supply is negligible. We can now consider cells with an internal resistance $r$. This is due to the resistance of the components inside a battery.
  
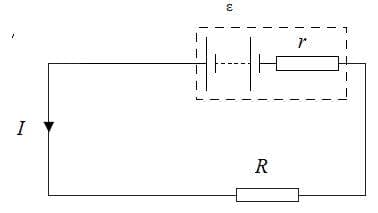
  The potential difference across the battery; the terminal potential difference:
  $\rm V = \varepsilon – Ir$
• The potential difference across the battery is equal to the emf when the current in the circuit is zero.
• The total electrical power by the battery $\rm = \varepsilon I$
• Electrical power dissipated in a resistor $\rm = VI = I^2R = V^2/R$
• When current is drawn from a cell, the terminal potential difference varies with time.
  The terminal potential difference of a typical cell:
  • Falls quickly from its initial value and then stays stable for most of its lifetime.
  • It then decreases rapidly to zero as the cell discharges.
• The emf and internal resistance of a cell can be determined from the following circuit:
  
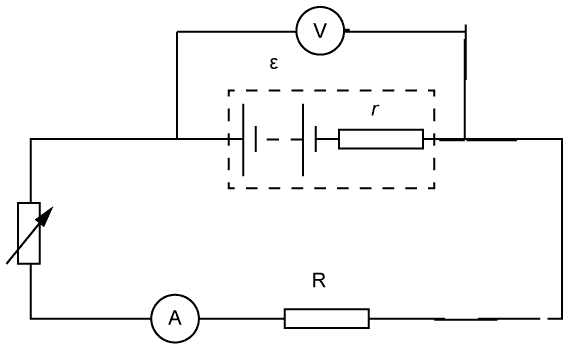
  The current is varied using the variable resistor and the terminal potential difference is measured.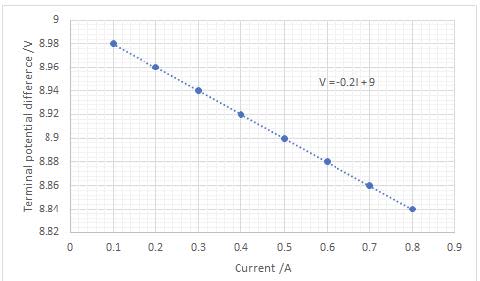
  
• The emf is given by the vertical intercept: in this case $\rm \varepsilon = 9.0~ V$
• The internal resistance is equal to the gradient; in this case $\rm r = 0.2~\Omega$.

• When cells are in series the voltage increases when they are connected in the same direction or decreases if they are connected in the opposite direction.
  

  $\rm \varepsilon_{total} = \varepsilon_1 + \varepsilon_2$ The current flows to the left.
  $\rm\varepsilon_{total} = \varepsilon_1 - \varepsilon_2$ The current flows to the left when $\rm \varepsilon_1 > \varepsilon_2$ and the right when $\varepsilon_1 < \varepsilon_2$

• When cells are in parallel the current increases when they are connected in the same direction.
  When identical cells are in parallel
  εtotal = ε but I = I1 + I2
  When unlike cells are connected there are no simple relationships and Kirchhoff’s laws have to used.
  

• A primary cell can only be used once (until it runs out) and is then discarded.

• A secondary cell is a cell that is rechargeable and can be used repeatedly.

Magnetism arises when one charge moves in the vicinity of another moving charge.

• The poles of a magnetic are called north-seeking and south-seeking because they point in those directions if suspended. Magnets have dipoles: as north or south seeking poles cannot exist in isolation.
• A magnetic field is a region of space where a ‘test’ magnet would experience a force. The field or flux lines show the direction of a force on the test’ magnetic north seeking pole if placed at that point.
• The strength of the force at a point is shown by the density of lines at the point.
  
• A similar magnetic field is produced when an electric current passed through a solenoid. The magnetic field pass through the inside of the solenoid from left to right.
  
• The current in a wire produces a magnetic field: a series of concentric circles. The direction of the field is reversed when the direction of the current is reversed.
  
• A magnetic field $\rm B$ exerts a force on moving charges given by $\mathrm F = qv\rm B \sin \theta$
  
  $\Theta$ is the angle between field and the velocity vectors.
• The force on electric currents given by $\rm F = BIL \sin \theta$.
  
  $\Theta$ is the angle between field and the current.
• The directions can be predicted by the thumb, first finger and second finger of the left hand. The Left Hand Rule $\rm (LHR)$.
  

• As the magnetic force is always normal to the velocity of the charge it follows that it cannot do any work.