Doppler effect

The Doppler effect describes the wavelength/frequency shift when relative motion occurs.

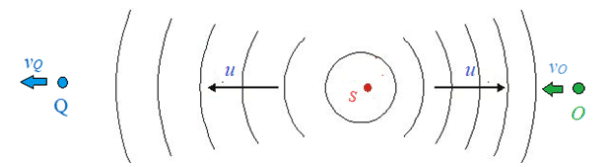
The Doppler effect is the change in the observed frequency of a wave whenever there is relative motion between the source and the observer.

• The siren of a fire engine police car is heard at a higher frequency when it approaches and at a lower frequency when it moves away. The wavefronts are squashed together as the source approaches and more separated as it moves away.
• Consider a source, $\mathrm{S}$, moving towards an observer, $\mathrm{O}$, and away from an observer $\mathrm{Q}$, with the speed $v_{s}$.
  
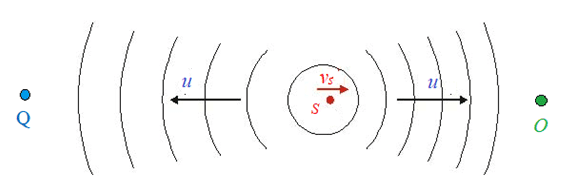
  In 1 sec f waves are emitted
  For Q (receding source):
  The wavelength $\lambda_{\mathrm{D}}=\left(u+v_{\mathrm{s}}\right) / f$ The observer at $\mathrm{Q}$ hears a sound of a lower frequency. The sound waves travel at speed u which is unchanged by the motion of the source):
  $f_{\rm D}=u / \lambda_{\rm D}$
  $=u f /\left(u+v_{s}\right)$
  For O (approaching source):
  The distance between the first and last waves:
  The wavelength $\lambda_{\mathrm{D}}=\left(u-v_{s}\right) / f$
  The observer at $\rm O$ hears a sound at higher frequency. The sound waves travel at speed u which is unchanged by the motion of the source):
  $f_{\mathrm{D}}=u / \lambda_{\mathrm{D}}$
  $f_{\rm D}=u f /\left(u-v_{s}\right)$
  (If you are unsure which formula to use, remember the frequency increases if the source is approaching and decreases when the source is moving away.)
• Consider the case of a source approaching an observer with a velocity at an angle θ to the observer.
  
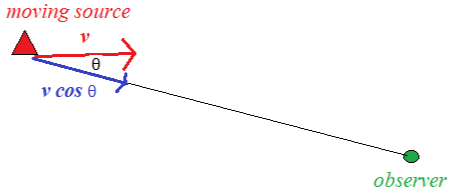
  $v \cos \theta$ is the component of the velocity in the direction of the observer.
  When the moving source is approaching.
  $f_{\mathrm{D}}=uf /\left(u-v_s\right)$
  $f_{\mathrm{D}}=uf /(u-v \cos \theta)$
  When the source is passing the observer $\left(\theta=90°\right) f_{\mathrm{D}}=f$
  When the moving source is moving away.
  $f_{\mathrm{D}}=uf /(u+v \cos \theta)$
• The graph below shows the frequency changes with time as the sou rce approaches and then moves away.
  
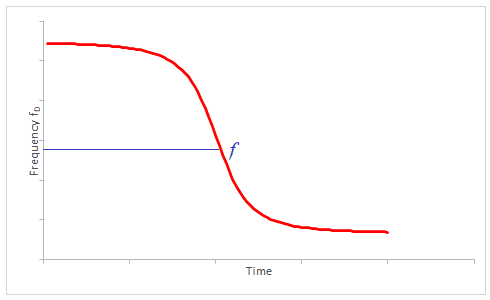
  The frequency, $f_{\rm D}$, heard is the same as the emitted frequency, $f$, when the source passes the observer.

• Consider an observer, $\rm O/Q$ moving towards/away from a source, $\rm S$, which emits sound with a speed $u$.
  
  For $\bf Q $ (receding:
  Speed of the waves relative to the observer
  $v'=u-v_{\mathrm{Q}}$
  $f_{\mathrm{D}}=\mathrm{V}' / \lambda$
  $f_{\rm D}=\left(u-\mathrm{V}_{\mathrm{O}}\right) f / u$
  For $\bf O$ (approaching observer):
  Speed of the waves relative to the observer:
  $v'=v_{\rm Q}+u$
  $f_{\rm D}=v' / \lambda$
  $f_{\rm D}=\left(v_{\rm O}+u\right) f / u$
• The Doppler effect has many applications. It can be used to measure the speed of cars, or the speed of blood cells.

Worked Example

The police use the Doppler effect to measure the speed of cars, A sound wave of frequency $12~000 \mathrm{~Hz}$ is directed at an approaching car. The reflected wave has a frequency of $\rm 13~000 ~Hz$. Determine the velocity of the car.
The speed of sound is $340 \mathrm{~m} \mathrm{~s}^{-1}$.

Solution

There are two Doppler shifts to consider.

1. 1The car is approaching the source so the frequency it receives is:
   $f=12~000 \times\left(340+v_{\rm car}\right) / 340 \mathrm{~Hz}$
2. The car is the source of the reflected wave which is measured by the police to have a frequency of $1~3000 \mathrm{~Hz}$.
   $13~000=340 /\left(340-v_{\text {car }}\right) f$ $=\left(12~000 \times\left(340+v_{\text {can }}\right) / 340\right) \times\left(340 /\left(340-v_{\text {car }}\right)\right)$ $=12~000 \times\left(340+v_{\text {car }}\right) /\left(340-v_{\text {car }}\right)$
   $13~000 \times\left(340-v_{\text {car }}\right)=12~000 \times\left(340+v_{\text {car }}\right)$
   $25~000 \times v_{\text {car }}=340 \times(1~000)$
   $v_{\text {car }}=340 \times(1~000) / 25~000$ $=13.6 \mathrm{~ms}^{-1}$
   We see here that speed of the car is given by the formula:
   $v_{\text {car }}=$ speed of sound $\times$ Change in frequency $/$ sum of frequencies
   $v_{\text {car }}=u \times \Delta f /\left(f_{1}+f_{2}\right)$

• When a light source approaches the frequency increases, and the wavelength decreases. This is a blue-shift. 
• When a light source moves away the frequency decreases and the wavelength increases. This is a red-shift. The magnitude of the red shift can be used to calculate the recessional velocity and provides evidence for the Big Bang model for the creation of the universe.
• The equations for the frequency observed are different from sound as the speed of light does not change with the relative motion of the observer from relativity theory. 
• If the speed of the source v or the observer is small compared to the speed of light, $c$, the equation takes a simple form:
  $\dfrac{\Delta f}{f} = \dfrac{\Delta \lambda}{f\lambda} = \dfrac{v}{c}$
  $\Delta f$ is the change in the observed frequency.
  $\Delta \lambda$ is the change in the observed wavelength.