Discrete energy and radioactivity

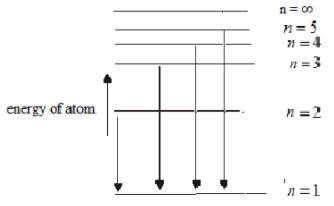
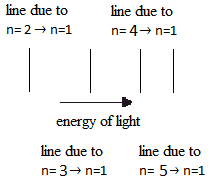In the microscopic world energy is discrete. It is carried in packets or quanta.

Spectra

• Light can be considered to be a wave or a particle. Particles of light are called photons.
• The electromagnetic spectrum includes in order of increasing frequency/energy: radio waves, microwaves, IR radiation, visible light, ultraviolet radiation X-rays, and $\gamma$ rays.
• The frequency $(f)$ and wavelength $[\lambda]$ of electromagnetic radiation are related by: $\mathrm{c}$ (speed of light $)=\lambda f$.
• The energy of a photon of light $E_{\text {photon }}$ is related to the frequency $(f)$ of the radiation by Planck's equation:
  $\mathrm E_{\text {photon }}=h f= \dfrac{h c}{\lambda}$
  $h$ is Planck's constant: $6.63 \times 10^{-34} \mathrm{Js}$ and $c$ is the speed of light $=3.00 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}$
• A continuous spectrum contains radiation of all wavelengths within a given range (e.g. the visible spectrum).
• A line spectrum consists of a mixture of discrete lines of different wavelengths/frequencies.

• Gases produce a characteristic emission line spectrum when they are heated to a high temperature.
• A photon of light is emitted when an electron falls from an excited state to a lower energy level. The energy of the photon corresponds to the energy change of the electron.
  $\mathrm E_{\text {photon }}=\Delta \mathrm E_{\text {electron }}$
• A line emission spectrum provides evidence for electrons occupying discrete energy levels. Each line is produced when an excited electron falls between different energy levels.
  For example, for a hydrogen atom:

Energy levels of hydrogen atom	Lines in the emission spectra (Lyman series)

• The energy levels of the hydrogen atom converge at higher energy as they are further from the nucleus, and the lines in the spectrum also converge at higher energy/frequency.
• The limit of convergence $n=\infty$ corresponds to the electron leaving the atom. The energy between the $n=1$ and $n=\infty$ energy levels are called the ionisation energy.
• The electronvolt is often used for atomic energy levels. $1 \mathrm{eV}=1.60 \times 10^{-19} \mathrm{~J}$

• An absorption spectrum is produced when white light is transmitted through a gas. The wavelengths corresponding to the emission line wavelengths are missing in the transmitted light.
• Electrons in the atoms of hydrogen absorb the photons with energies corresponding to the frequencies in the emission spectrum and make transitions from a lower to a higher energy state.
• An absorption spectrum is like a "negative" of an emission spectrum and consists of a series of dark lines against a coloured background.

• The atom consists of the three subatomic particles:

• The proton or atomic number, $\mathbf{Z}$, is defined as the number of protons in the nucleus of the atom. It is also the number of electrons in a neutral atom.
• The nucleon or mass number, $\mathbf{A}$, is the number of protons plus the number of neutrons in the nucleus as both contribute to the overall mass of the atom. Protons and neutrons are collectively called nucleons.
• A particular nucleus of a chemical element $\rm X$, with $\rm Z$ protons and $\rm A$ nucleons is represented as $\rm ^A_Z X$.

A simple model of a lithium atom

• A nucleus with a specific number of protons and a specific number of neutrons is called a nuclide.
• Nuclei with the same proton number but different nucleon numbers are called isotopes of each other. $^1_1 \mathrm{H}, ^2_1 \mathrm{H}$, and $^3_1 \mathrm{H}$ are all isotopes of hydrogen.
• Isotopes have the same chemical properties (same number of electrons) but different physical properties (e.g. different mass, nuclear radii, specific heat capacity).
  The approximate mass of a nucleus of nucleon number $\rm A$ is $\rm A$ atomic mass units $\rm (u)$.
• $1 \mathrm{u}=1.66 \times 10^{-27} \mathrm{~kg}$. The $\mathrm{u}$ is $\dfrac{1}{12}$ of the mass of the neutral atom of the carbon isotope $^{12}_6 \mathrm{C}$

• There are four fundamental forces in nature:
  • Electromagnetic: (Topic 5) which acts on particles with charge. The force has infinite range. ($\mathrm{F}_{\mathrm{e}} \propto \dfrac{\rm Q_1 Q_2}{d_2}$ and is $0$ when $\mathrm{d}$ is infinite).
  • Gravitational: (Topic 6) which is the force of attraction between masses. It is generally irrelevant for atomic and nuclear physics. This force has infinite range. $(\mathrm{F}_{\mathrm{g}} \propto \dfrac{M_1 m_2}{d 2}$ and is $0$ when $\mathrm{d}$ is infinite).
  • Weak nuclear interaction: which acts between particles (protons, neutrons, electrons and neutrinos) involved in beta decay. It has very short range $\left(10^{-18} \mathrm{~m}\right)$.
  • Strong nuclear interaction: which is a generally attractive force which acts on protons and neutrons inside nuclei. It has short range $\left(10^{-15} \mathrm{~m}\right)$.
• The dominant forces acting within a nucleus are:
  
  • the electrostatic repulsion force between the protons.
  • the strong nuclear force acting between nucleons.
• The presence of the strong nuclear force prevents the electrostatic repulsive force between neighbouring protons from pulling the nucleus apart.

More details are discussed later.

• The stability of a nucleus depends on the balance between the number of protons and the number of neutrons. 
• As the graph below shows for small proton numbers a nucleus is stable if it contains about the same number of protons and neutrons, but large nuclei require more neutrons than protons to be stable.

• The stability of a nucleus is determined by balance between the attractive and repulsive forces acting within the nucleus. If a nucleus contains too many protons compared to neutrons, the repulsive electrostatic forces are dominant, and the nucleus is unstable. Neutrons contribute to binding without contributing to the repulsive electrostatic force.
• As we will see later a nucleus can also be unstable if it contains too many neutrons compared to protons. A situation which leads to beta decay.
• Most nuclides are unstable and are radioactive. They decay by emitting particles which change the composition of the nucleus. 

• Most nuclei are unstable and decay into more stable nuclei by emitting alpha, beta or gamma particles.
• • Alpha particles are helium nuclei, $^4_2 \mathrm{He}$
  • Beta particles are fast electrons, $^0_{-1} e$ (beta minus decay) or positrons $^0_{+1} e$ (beta plus decay see next section).
  • Gamma particules are photons, $^0_0 \gamma$
• During alpha decay the proton number decreases by $2$ and the nucleon number by $4.$ $\rm ^A_Z X \rightarrow ^{A-4} _{Z-2} Y+ ^4_2 \mathrm{He}$
• During beta minus decay the proton number increases by $1$ and the nucleon number is unchanged. An antineutrino $(\nabla)$ is also produced (see next section), which has no mass or charge.
  $\rm ^A_Z X \rightarrow ^A_{Z+1} Y + ^0{-1} e + ^0_0 \nabla$
• In beta minus decay a neutron decays to a proton within the nucleus and the electron and antineutrino ( $\nabla)$ are emitted:
  $^1_0 n \rightarrow ^1_1 p+^0_{-1} e+^0_0 \nabla$
• The weak nuclear interaction acts on protons, neutrons, electrons and neutrinos in order to bring about beta decay.
• Gamma emission leads to a reduction in energy as the protons and neutrons change their relative positions often as a result of alpha or beta decay. The proton and nucleon numbers are not changed. The nucleus is said to change from an excited state to a lower energy state.
• Note the total charges (subscripts) and mass numbers (superscripts) are balanced in a nuclear reaction.
• Alpha, beta and gamma particles are ionising, as they produce ions by removing electrons when they collide with atoms.
• For the same energy, alpha radiation is the least penetrating and the most ionising, while gamma radiation is the most penetrating and the least ionising.
• Radioactive decay is:
  
  • random: it cannot be predicted when a particular nucleus will decay
  • spontaneous: it cannot be induced to happen or prevented from happening

• An antineutrino is an example of an antimatter particle.
• Every form of matter has its equivalent form of antimatter. If matter and antimatter come together they annihilate each other.
• The positron is the antimatter particles of the electron: when a positron and an electron collide they annihilate each other to produce two photons:
  $^0_{+1} \mathrm{e}+^0_{-1} \mathrm{e} \rightarrow 2^0_1 \gamma$
• The very early universe contained almost equal numbers of particles and antiparticles. But today we see matter and not antimatter.
• Another form of radioactive decay that can take place is beta plus or positron decay when a proton decays into a neutron with the production of a positron and a neutrino:
  $^1_1 \mathrm{p} \rightarrow ^1_0 \mathrm{n}+^0_{+1} \mathrm{e}+^0_0 \mathrm{~V}$
  For example potassium 40 undergoes beta plus decay to produced argon- 40 :
  $^{40}_{19} \mathrm{~K} \rightarrow ^{40}_{18} \mathrm{Ar}+^0_{+1} \mathrm{e}+^0_0 \mathrm{~V}$

• Although radioactive decay is random the rate of decay can be predicted.
• The rate of decay, or activity is proportional to the number of nuclei present $\rm (N)$ :
  $d\mathrm N / d t \propto \rm N$
• The activity $\rm (A)$ is the number of decays per second.
• There is an exponential decrease in activity with time.
• As activity $\rm (A)$ is proportional to the number of nuclei $\rm (N)$ it follows the same exponential decay law as the number of nuclei.
  The unit of activity is the becquerel: $\rm 1 Bq = 1$ decay per second.
• The time interval after which the activity of a sample is reduced by a factor of 2 is also constant and is called the half-life, $\bf T_{1 / 2}$
• The half-life is also the time taken for half the number of nuclides present in a sample to decay.

Worked example

The activity of a sample is initially $80$ decays per minute. It becomes $5$ decays per minute after $8 \mathrm{~h}$. Calculate the half-life.

Solution

The initial activity $\rm A_{0}=80 ~min^{-1}$ and activity after $4 \mathrm{~h}$: $\rm~A_{4h} = 5 ~min^{-1}$ $\rm A_{4h} / A_{0}=1 / 16=1 / 2^{4}$
The activity is reduced from $80$ to $5$ in $4$ half-lives. $4$ half-lives is $8 \mathrm{~h}$, so the half-life is $2 \mathrm{~h}$.

• The activity of a radioactive sample is measured using a Geiger counter, which detects and counts the number of ionizations. Some radioactive ionizations occur even when there is no identified radioactive source present: this background count is due to background radiation. 
• The background radiation includes cosmic gamma rays and $\alpha$, $\beta$ and $\gamma$ radiation from surrounding materials.
• To analyse the activity of a given radioactive source, it is necessary to correct for the background radiation taking place. The background count without the radioactive source present is subtracted from all readings with the source present.