Describing field

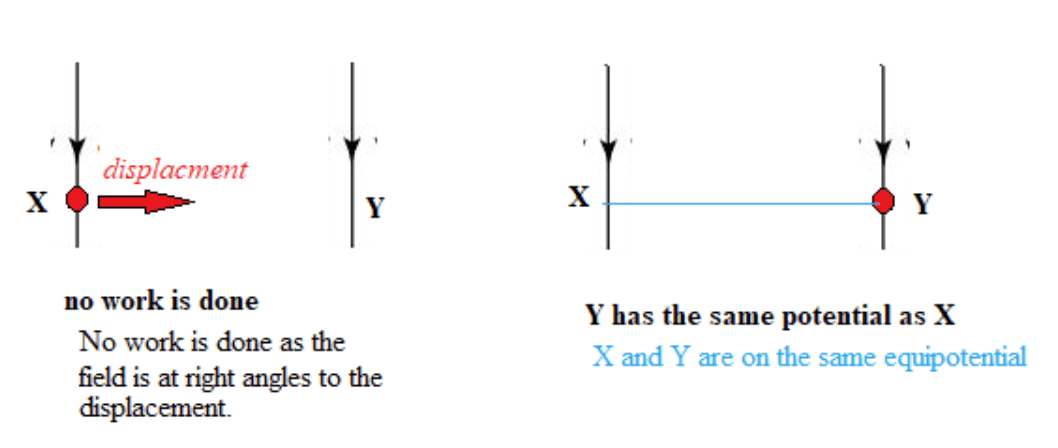
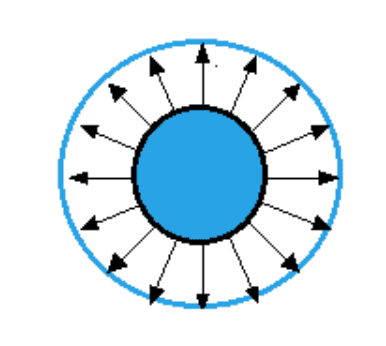
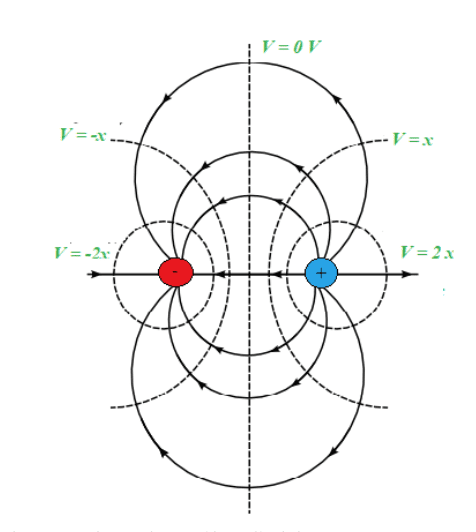
Electric charges and masses influence the space around them. This can be represented with h the concept of electric and gravitational fields.

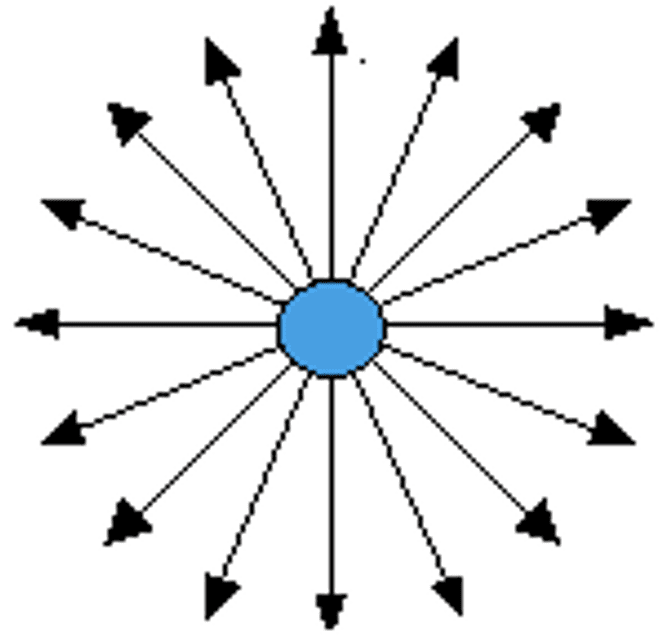
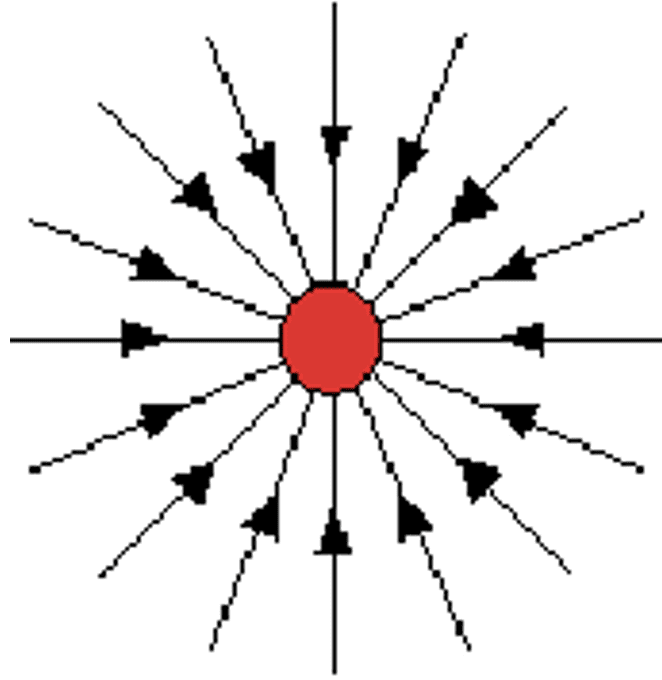
• A body of mass $\rm M creates a gravitational field in the space around it. This fields acts on other bodies by exerting a gravitational force.
• Gravitational field strength $(g) =$ force per unit test point mass $g =\mathrm F / m= \mathrm{GM}^{2}/r^{2}$
  $g$ has units: $\rm N~ kg ^{-1}$
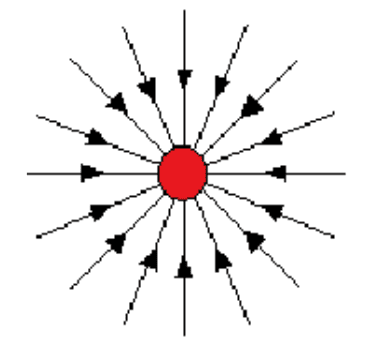
  It is a vector quantity.
• All masses are attracted towards the mass shown. Gravitational field lines end on masses.
  

• An electric charge $\rm Q$ creates an electric field in the space around it. This fields acts on other charges by exerting an electric force.
• The electric field $\rm (E)$ at a point is the electric force per unit charge exerted on a small, positive point charge $q$ placed at that point. It is a vector quantity.
  For a charge $\rm Q$:
  $\mathrm{E =F} / q = k \mathrm Q q / q r^{2}$ $= k \mathrm Q/ r^{2}$
  

  The electric field of a positive charge. The lines are outward as a test positive charge is repelled.	The electric field of a negative charge.  The lines are inward as a test positive charge is attracted.

• Electrostatic field lines start on positive charges and end on negative charges.

• Field strength is a vector. The direction of the field is shown directly and the magnitude of the field strength is represented by the closeness of the field lines.
• Field lines:
  • never cross
  • are close together when the field is stronger.
• Work is done when an object is moved along a field line, but not if an object is moved at right angles to a field line. $\rm Work = F~s \cos\theta = 0$ when $\theta = 90°$.
• As no work is done when an object moves at right angles to a field line there is no change in potential at right angles to a field line.

Gravitational potential

• The Gravitational potential $\bf(V_g)$ due to a mass $\rm M$ is the work done $\rm (W)$ by an external force per unit mass in moving a point mass $\rm (m)$ from infinity to a point near the mass $\rm M$.
  $\rm V_g = W/m$
• The unit of gravitational potential is $\rm J~ kg^{-1}$.
• The gravitational potential $(\mathrm V_g)$ at a distance, $r$, from a particle of mass, $\rm M$, $\mathrm V_g = -\mathrm{GM}/r$
• As the mass $m$ is naturally attracted to $\rm M$ the work done is always negative.
• The work done in moving a mass $\rm m$ from $\rm A$ to $\rm B = m(V_g{^B}– V_g{^A}) = m\Delta V_g{^{BA}}$

Electric potential

• The Electric potential $\bf (V_e)$ due to a charge $\rm Q$ is the work done $\rm (W)$ by an external force per unit charge in moving a (positive) point charge $(q)$ from infinity to a point near the charge $\rm Q$.
  $\rm V_e = W/\cal q$
• The unit of electric potential is the volt $\rm (V)$ which is equivalent to $\rm J ~C^{-1}$.
• The electric potential $\rm (V_e)$ a distance $r$ from a body of charge $\rm Q$, $\mathrm{V_e} = \mathrm Q/r = \mathrm Q/4\pi \varepsilon r$.
  The sign of the potential depends on the sign of the charge.
• When $\rm Q$ is positive there is repulsion between $\rm Q$ and the test charge $q$ and the work done is positive. When the $\rm Q$ is negative there is attraction between $\rm Q$ and the test charge $q$ and the work done is negative.
• The work done in moving a charge $(q)$ from $\rm A$ to $\mathrm B = q\rm (V_e{^B} – V_e{^A})$ $= q \rm \Delta V_e{^{BA}}$

Gravitational and electric potential are both scalar quantities. To find the potential due to several masses or charges we simply need to add the potential due to each separate mass/charge.

• Equipotential surfaces link points with the same potential. Equipotentials are at $90°$ to field lines.
  
• An equipotential surface in blue for a spherical mass or charge. 
• Note there are no field lines in the body.
  

• Equipotential surfaces for a positive charge and negative charges (dotted lines).
• Note the field lines are at right angles to the equipotential surfaces.
  

• Field lines and equipotential surfaces can both be used to describe fields. 
• Equipotential lines cannot cross as one point cannot have two different potentials!
• The work done in moving a charge $(q)$ from $\rm A$ to $\mathrm B = q \Delta \rm V _e{^{BA}}$ $=- q \Delta \rm V _e{^{ AB}}$ $= \mathrm F \Delta x$
  $\mathrm F \Delta x =- q \Delta \rm V_e{^{AB}}$
  $\mathrm F / q = -\Delta \mathrm{V_e{^{AB}}} / \Delta x$
  $\rm E =-\Delta V_e{^{AB}} / \Delta \mathcal x$
  $\rm E =-\Delta V_e / \Delta \cal x$