In the previous chapter we discussed how to find a function, given the derivative of the function. We will continue to build upon that in this chapter.
Recall: Given a polynomial of the form: $f'(x)=ax^n$ then an antiderivative of $f(x)$, is:
$f(x)=\dfrac{a}{n+1}𝑥^{n+1}$
Without going into a formal proof, the total change in a system can be represented as the area between the curve and the $x-$axis between $x=a$ and $x=b$. This is referred to as a definite integral. It is calculated by finding the anti-derivative of a function and evaluating it between two $x$ values. Mathematically speaking:
$\displaystyle \int^b_a f(x)\mathrm dx=\mathrm F(b)−\mathrm F(a)$ where $a < b$ and $\mathrm F(x)$ is the antiderivative of $f(x)$.
Example 1: Evaluate $\displaystyle \int^2_0(x^2+x)\mathrm dx$
Explanation: Since the antiderivative of $x^2+x=\dfrac{x^3}{3} + \dfrac{x^2}{2}$, then:
$\displaystyle\int^2_0(x^2+x)\mathrm dx =\dfrac{x^3}{3} + \dfrac{x^2}{2} \overset{|^2}{|_0}$
$= \dfrac{2^3}{3} + \dfrac{2^2}{2} − \left(\dfrac{0^3}{3}+\dfrac{0^2}{2}\right)$
$=\dfrac{8}{3} + 2−(0+0)=\dfrac{14}{3} = 4.67$
This can be seen in the following graph as the area under the curve of $x^2+x$ and above the $x-$axis between $x=0$ and $x=2$ using the 2nd TRACE command and option 7 on the TI-84 CE graphing calculator.
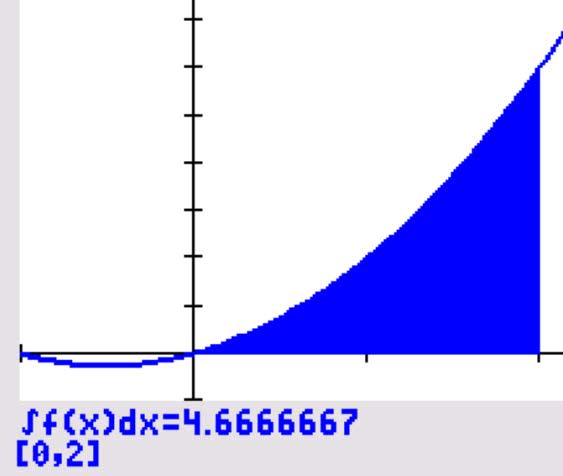
Example 2: Evaluate $\displaystyle\int^{\pi}_0(\sin(2x) + 2)\mathrm dx$
Explanation: Since the antiderivative of $\sin(2x) = −\dfrac{1}{2}\cos(2x)$, then:
$\displaystyle\int^{\pi}_0(\sin(2x) + 2)\mathrm dx = −\dfrac{1}{2} \cos(2x) + 2x \overset{|^{\pi}}{|_0}$
$= −\dfrac{1}{2}\cos(2\pi) + 2\pi − \left(−\dfrac{1}{2} \cos(2(0)) + 2(0)\right)$
$= − \dfrac{1}{2} (1) + 2\pi − \left(− \dfrac{1}{2} (1) + 0\right)$
$= − \dfrac{1}{2} + 2\pi + \dfrac{1}{2} = 2\pi \approx 6.28$ square units
Again, this can be seen in the following graph using the TI-84 CE graphing calculator, making sure the calculator is in Radian Mode:
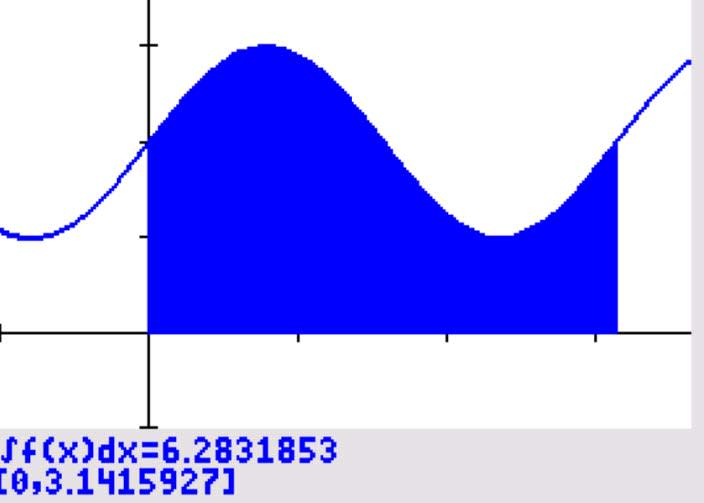
 Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
Nouveau ! Découvrez Nomad'IA : le savoir de nos 400 profs + la magie de l'IA
